Måling og reduksjon av risiko i finansielle investeringer ved tilstandsavhengig avkastning
Finanskrisen viste at vesentlige sider ved den datagenererende prosessen for finansiell avkastning ikke ble fanget opp av det eksisterende analyseverktøyet, slik at sannsynligheten for markedsuro – med påfølgende store tap – ble undervurdert. Bidraget i artikkelen er en konseptuell modell, som er variant av såkalt «Value at Risk targeting». Modellen demonstrerer hvordan porteføljens halerisiko kan kontrolleres når: i) Avkastningens momenter er tilstandsavhengige; ii) Risikoen for store tap øker drastisk i perioder med usikkerhet og stress i markedene. I motsetning til den mye brukte Value at risk-metoden spesifiseres det i utgangspunktet en maksimal tapsverdi – en kvantil i en sannsynlighetsfordeling – som må tilfredsstille en gitt risikotoleranse, spesifisert i form av en halesannsynlighet. Risikoen kontrolleres ved å inkludere en tilstrekkelig andel av risikofrie aktiva, slik at sannsynligheten for tap utover maksimal tapsverdi ikke overskrides. Denne andelen bestemmes av kritisk tapsverdi, risikotoleransen og de langsiktige sannsynlighetene for hhv. oppgangs- og nedgangsperioder. Fremgangsmåten for numerisk optimering av problemet i Excel er vist i et appendiks. Et sekundærbidrag er en skisse av hvordan metoden kan anvendes til å håndtere likviditetsrisiko i banksektoren, slik at Baselregelverkets likviditetskrav overholdes.
Måling og reduksjon av risiko i finansielle investeringer ved tilstandsavhengig avkastning1
Innledning
Tilgang på finansiering er en grunnleggende forutsetning for moderne markedsøkonomier. Dessverre ser det ut til at finansmarkedene også har en uheldig side ved at de kan bidra til oppbygging av prisbobler og gjeld, og dermed økonomisk sårbarhet som kan resultere i etterspørselssvikt og krise i realøkonomien. Overoptimisme nevnes i litteraturen som en mulig årsak til pris- og gjeldsoppbyggingen i forkant av kriser.2. Av den grunn er risikostyring i finansmarkedene av største betydning for økonomisk stabilitet i samfunnet som helhet. Et velkjent finansteoretisk prinsipp for kontroll og reduksjon av risiko uten at det går på bekostning av forventet avkastning, er diversifiseringsprinsippet. Det vil si å spre sine risikable verdipapirer på objekter hvis verdiutvikling ikke går i takt. Diversifiseringsprinsippet fungerer så lenge avkastningens statistiske momenter er noenlunde stabile og ikke brått endrer seg i ugunstig retning. Det er imidlertid empiriske holdepunkter3 for å hevde at momenter, slik som forventet avkastning, varians, korrelasjon, skjevhet og kurtosis er asymmetriske og tilstandsavhengige, og at disse øker til dels kraftig i perioder med stor usikkerhet og markedsuro (bear markets). Dersom samvariasjon (korrelasjonen) øker ved markedsuro, betyr det at diversifiseringsprinsippet bryter sammen når det trengs som mest, slik som under utbruddet av finanskrisen i 2008. Finansteorien må derfor utvides slik at den besvarer følgende spørsmål, hvilket også er den grunnleggende problemstillingen i denne artikkelen:
- Hvordan måle og kontrollere risiko i finansielle porteføljer gitt at avkastningens datagenererende prosess kjennetegnes ved skifte av sannsynlighetsfordeling, avhengig av om økonomien er i ekspansjons- eller kontraksjonsfase? Vi vil også karakterisere de ulike fasene mht. forventet avkastning og risiko, og hvor hyppig de risikoøkende kontraksjonsfasene forekommer, målt ved de langsiktige sannsynlighetene.
Avgrensingen av problemstillingen tar utgangspunkt i to relativt nye retninger i litteraturen (se litteraturkapitlet for referanser) som tar for seg reduksjon av markedsrisiko:
- Volatility targeting, hvor man forsøker å sette sammen en portefølje med en predefinert konstant risiko (målt ved avkastningens standardavvik, også kalt volatilitet), og
- Value at Risk targeting, også kalt «tail risk targeting», som kan oversettes med mål for halerisiko. Dette går ut på at halerisikoen i porteføljen – målt ved en kvantil i sannsynlighetsfordelingen for porteføljens avkastning – forsøkes holdt konstant, og som er betinget på en forhåndsbestemt sannsynlighet (dvs. risikotoleranse) for at et slikt tap skal inntreffe i løpet av investeringshorisonten. Dette er en variant av den mye brukte metoden Value at Risk (VaR), men hvor man i utgangspunktet setter en grense på porteføljens VaR. Ved et halerisiko-mål settes altså en bestemt grense for det potensielle tapet (en kritisk tapsverdi, KTV) i løpet av en viss periode, og med en viss sannsynlighet for å inntreffe. En kan f.eks. si at tapet ved utløpet av holdeperioden ikke kan overstige 15 prosent av porteføljeverdien (KTV = minus 15 prosent), og at sannsynligheten for dette skal være 1 prosent. Det vil si at man vil være 99 prosent sikker på at porteføljeverdien er minst 85 prosent ved utløpet av holdeperioden.
Ved å øke andelen av et risikofritt aktivum, kompenseres det for det faktum at det klassiske diversifikasjonsprinsippet bryter sammen pga. at korrelasjoner øker under markedsuro. Av grunner som utdypes nedenfor tar denne artikkelen utgangspunkt i stabilisering av halerisiko, dvs. VaR targeting,og utvikler en enkel konseptuell modell for å redusere porteføljerisikoen når avkastningens momenter varierer.
- Som et spesifikt hovedbidrag er det dokumentert, med detaljerte utregninger i et praktisk eksempel, hvordan man kan redusere risikoen i en portefølje under restriksjonene av en gitt maksimal (kritisk) tapsverdi og et gitt konfidensnivå, samt at porteføljens avkastning følger en bivariat normal blandingsfordeling med tilstandsavhengige (Markovskiftende) parametere. Bidraget kan klassifiseres som «VaR targeting med normal blandingsfordeling og Markovskiftende parametere», hvilket til min beste kunnskap ikke er belyst tidligere.
- Et tilleggsbidrag er en skisse av hvordan metoden kan brukes til å håndtere likviditetsrisiko i banksektoren, ved å sette sammen en handelsportefølje av risikable og risikofrie aktiva slik at Baselregelverkets likviditetskrav (jfr. «liquidity coverage ratio») overholdes. Dette antas også å være et unikt bidrag.
Det er flere grunner til å foretrekke styring av halerisiko fremfor styring av volatilitet, og disse gjennomgås nærmere i litteraturkapitlet. Når det gjelder anvendelser er modellen relevant både for småsparere, bedrifter og finansinstitusjoner, ikke minst for banksektoren med tanke på beregning av kapitalkrav og likviditetsstyring. En bank, men også andre bedrifter og privatpersoner, må sikre seg at balansen består av tilstrekkelig likvide aktiva i urolige tider, slik at løpende forpliktelser kan innfris. Banksektoren er spesielt viktig for økonomisk stabilitet, siden denne sektoren er den viktigste finansieringskilden for både husholdninger og bedrifter, og dermed for samfunnet som helhet. Dersom andelen av risikable aktiva i banksektoren er høy når nedgangstider inntreffer, kan en økning i samvariasjon medføre et synkronisert verdifall i hele sektoren, slik at flere banker blir insolvente. Dette truer den økonomiske stabiliteten, slik man opplevde under finanskrisen. For å unngå slike kriser har den såkalte Basel-komitéen for banktilsyn (Basel Committee on Banking Supervision, BCBS) derfor utarbeidet et strengere regelverk for beregning av både kapital- og likviditetskrav, der konvergens av korrelasjoner under markedsstress hensyntas, jfr. Basel Committee on Banking Supervision (2011, 2019a, 2019b) . Artikkelen foreslår derfor en mulig anvendelse med hensyn til likviditetsrisiko i banksektoren, der det skisseres hvordan metoden kan brukes til å sette sammen en handelsportefølje av risikable og risikofrie aktiva slik at Baselregelverkets likviditetskrav (jfr. «liquidity coverage ratio») overholdes. Metoden vil også kunne egne seg til aktiv forvaltning av oljefondet, for derved å unngå store svingninger i verdiutviklingen til fondet.
VaR targeting kan innebære grader av dynamisk (aktiv) justering av porteføljer, dvs. at blandingsforholdet av risikable og risikofrie verdipapir varierer. I denne artikkelen forutsettes det imidlertid at man beregner og benytter de – antatt relativt stabile – langsiktige sannsynlighetene for oppgang og nedgang sammen med de tilhørende forventede momenter for avkastningen, og ikke forsøker å time markedet mht. når et skifte i markedsregime forekommer. Ved bruk av normal blandingsfordeling, som i denne artikkelen, ville det medføre ustabilitet i selve blandingsfordelingen (se utledningen av normal blandingsfordeling i seksjon 4.1) og dermed ville hele poenget med stabilisering forsvinne. Således blir metoden passiv mht. overgangssannsynligheter, og tilstandsavhengig forventet avkastning og varians for enkeltaktiva. Men sammensetningen av den risikable porteføljen kan naturligvis varieres fritt. I tillegg er det mulighet for diskresjon mht. risikotoleransen, dvs. halesannsynligheten man vil kontrollere. Dersom metoden benyttes i banker og finansinstitusjoner må regulerende myndigheter bestemme risikotoleransen, hva som kan regnes som rimelige estimater, og om ny informasjon tilsier at det er rimelig å endre oppfatning om hva de langsiktige parameterverdiene bør være. I seksjon 4.1 gis eksempler på estimater av tilstandsavhengige sannsynlighetsfordelinger for aksjeindekser i Norge og USA, og hvor ofte tilstandene oppgang og nedgang i gjennomsnitt forekommer.
Artikkelen fortetter slik. Neste seksjon går gjennom relevant litteratur på området. Først ser vi på stiliserte fakta for finansiell avkastning, og hvordan disse underbygger valg av sannsynlighetsfordeling i analysen. Dernest beskrives konseptet VaR targeting («tail risk targeting»), i denne artikkelen oversatt og omdøpt til «Kritisk tapsverdi» (KTV). Seksjon 3 repeterer beregningen av VaR for en enkel portefølje av et risikabelt og et risikofritt aktivum, under den forenklende forutsetningen om normalfordelte data. Samtidig gjennomgås en del begreper som vi får bruk for senere i artikkelen. Seksjon 4 viser beregningen av KTV i en portefølje bestående av aksjer og risikofri rente, først med den forenklende forutsetningen om normalfordelt avkastning, deretter med den antatt mer realistiske antakelsen om at avkastningen følger en bivariat normal blandingsfordeling, dvs. med to tilstander. Disse er hhv. «oppgang» (tilstand 1) og «nedgang» (tilstand 2). Seksjon 5 skisserer et eksempel på hvordan metoden kan benyttes for å tilfredsstille likviditetskrav i banksektoren etter Baselregelverket, mens seksjon 6 oppsummerer, konkluderer og foreslår tema for videre forskning.
Teori og litteratur
Diversifiseringsprinsippet under markedsuro
Å spre sine investeringer på flere objekter, såkalt diversifisering, er et gammelt og grunnleggende prinsipp. Fra litteraturen kjenner vi for eksempel til Forkynnere (Ecclesiastes), hvis skrifter utgjør en av de 24 bøkene i den hebraiske bibelen, og som også hører med til visdomsbøkene i Det Gamle Testamente4, hvor det oppfordres til å spre sine investeringer, fordi man ikke vet hvilken risiko fremtiden vil bringe. Et annet eksempel er Shakespeares Antonio i «Kjøpmannen i Venedig», som ikke er bekymret for sine investeringer siden de er spredt på flere objekter (i dette tilfellet i lasten på fire skip som skulle til ulike havner). Rasjonalet som ligger til grunn er at med flere ulike investeringsobjekter vil det være mindre sannsynlig at verdiene på de enkelte objekter beveger seg i samme retning, eller at alle skipene synker, som i Antonios tilfelle. Det vil med andre ord være mindre sjanse for å tape alt dersom man har flere ulike objekter i porteføljen, og ikke bare ett.
Diversifiseringsprinsippet ble formalisert i en matematisk modell av Harry Markowitz (1952). Denne modellen, kjent som «Moderne Porteføljeteori» (MPT), viser hvordan en porteføljes varians (en proxy for risiko) avhenger av samvariasjonen (målt ved kovariansen eller korrelasjonen) mellom avkastningen til objektene i porteføljen. Ved å sette sammen en portefølje der objektene har lav kovarians kan man redusere porteføljerisikoen betraktelig. MPT bygger på beregning av to spesifikke parametere: porteføljens forventede avkastning og volatilitet5. For å illustrere betydningen av samvariasjon, i en portefølje med to risikable aktiva X og Y er forventet porteføljeavkastning E(Rp) og porteføljevarians σp2 gitt ved følgende uttrykk:
1)
hvor og er forventet avkastning for hhv. X og Y, og v er andel av samlet beløp investert i X. Porteføljevariansen er gitt ved
,2)
hvor , er de respektive individuelle varianser, og er kovariansen mellom X og Y. Denne kan også skrives ved hjelp av korrelasjonen mellom og , :
3)
hvor er de respektive standardavvik. Korrelasjonskoeffisienten er et tall mellom minus 1 og pluss 1. Det følger at diversifiseringsprinsippet i økende grad bryter sammen dersom faktorene i ligning 3 øker under markedsuro, spesielt dersom korrelasjonskoeffisienten skifter fortegn fra minus til pluss og nærmer seg 1.
Campbell and Hentschel (1992), Harvey og Siddique (1999), Jondeau og Rockinger (2003) og Bali et al. (2008) viser at momentene skjevhet og kurtose er tidsvarierende, og slik at stor negativ avkastning i ulike aktiva tenderer til å forekomme samtidig. Ehling og Heyerdahl-Larsen (2014, s. 1919) finner at den gjennomsnittlige korrelasjonen i amerikanske industriporteføljer samvarierer med gjennomsnittlig aksjeavkastning, samt at det er store variasjoner i korrelasjon, volatilitet og forventet avkastning i nedgangstider, og som skaper signifikante behov for rebalansering av porteføljer. Chabi-Yo et al. (2018) rapporterer at avhengigheten i venstrehalen i sannsynlighetsfordelingen til avkastningen på ulike aksjer er større enn avhengigheten i høyrehalen, og at denne avhengigheten øker i perioder med markedsturbulens6. Det vil si at aksjemarkedet som helhet tenderer til å krasje samtidig.
Finansiell avkastning, stiliserte fakta og valg av sannsynlighetsmodell
Forskningen ser ut til å være klar på at en enkelt normalfordeling gir en ufullstendig beskrivelse av finansiell avkastning, i alle fall for observasjonsfrekvenser vi vanligvis opererer med i finansiell analyse. Dette ble påpekt allerede på 1960-tallet av Mandelbrot (1963), spesielt på grunn av forekomsten av venstreskjevhet. Cont (2001 s. 224) lister opp egenskaper som typiske for denne type data, såkalte stiliserte fakta, basert på «et halvt århundre med empirisk forskning». Et utdrag av disse er :
- Fravær av autokorrelasjon: lineær korrelasjon i aktiva-avkastning er ofte ikke signifikant, med unntak av for svært korte observasjonsintervaller.
- Tunge haler.
- Asymmetrisk fordeling av gevinst/tap («skewness», eller skjevhet): fordelingen er typisk venstreskjev, med større sannsynlighet for store tap enn for store gevinster.
- Opphopning av volatilitet («volatility clustering»): det er positiv autokorrelasjon i variansen (standardavviket) til avkastningen, slik at det oppstår perioder med høyere varians (standardavvik).
- Autokorrelasjon i absolutt avkastning. Her avtar autokorrelasjonen sakte, hvilket kan tolkes som en form for avhengighet over tid. Denne egenskapen kan også ses i sammenheng med «volatility clustering» siden absolutt avkastning omfatter både positiv og negativ avkastning.
Forskning på statistiske egenskaper for avkastning er nødvendig, sier Cont (s. 226) ikke bare for risikostyring generelt, men særlig for beregningen av Value at Risk, som er et utgangspunkt for å estimere behovet for lovpålagt sikkerhetskapital i finansielle institusjoner, og som krever bruk av en sannsynlighetsfordeling. Mange tilnærminger eksisterer på dette området, og bruk av såkalte ekstremverdi-fordelinger er mye brukt, samt ulike asymmetriske fordelinger. Såkalte «normal mixtures» (heretter kalt normal blandingsfordeling, forkortet til NBF), dvs. sannsynlighetsvektede blandinger av ulike normalfordelinger, er blitt populære i den senere tid. Dette på grunn av evnen til å gjenskape stiliserte fakta som tunge haler, skjevhet og opphopning av volatilitet. For eksempel testet Schaller og Van Norden (1997) eksistensen av tilstandsavhengig avkastning i en Markovskiftende modell med to ulike normalfordelinger, og konkluderte (s. 177) at: «… very strong evidence is found for switching behaviour». Rydén et al. (1998) finner at NBF evner å reprodusere stiliserte fakta i daglige avkastningsdata.
En NBF benyttes derfor i den følgende analysen i denne artikkelen. Et annet og viktig poeng som taler for NBF i forhold til andre asymmetriske fordelinger er at den er konsistent med eksistensen av ulike markedssentiment, dvs. veksling mellom optimisme og pessimisme. Sentimentet påvirker tilbud og etterspørsel i finansmarkedet, og dermed også avkastningen. Et overveiende optimistisk sentiment i oppgangstider kan således forklare oppbyggingen av prisbobler og gjeld, som medfører stor nedsiderisiko. Anvendelse av slike modeller i økonomimodeller forutsetter dermed at økonomiske data ikke er trukket fra en homogen populasjon, men kan deles inn i sentiment-baserte subpopulasjoner med hver sine karakteristiske parametere.
En bonuseffekt er at NBF’er er forholdsvis enkle å forstå siden de bygger på normalfordelingen, som er mer kjent enn andre typer fordelinger. Sannsynlighetsregning med NBF gir imidlertid utfordringer, siden det ikke finnes uttrykk som kan løses analytisk for å beregne halesannsynligheter. Dette krever optimeringsverktøy, men disse er innebygd i vanlige statistikkprogrammer. Denne artikkelen benytter både regnearket Excel og programmeringsverktøyet R.
Volatilitet vs. halerisiko
Metodene for kontroll av både volatilitet og halerisiko bygger som nevnt på porteføljer bestående av en kombinasjon av risikable og risikofrie aktiva. Ved volatilitetsmål settes en øvre grense på porteføljens standardavvik, som så forsøkes holdt konstant ved å øke eller redusere andelen av risikofritt aktivum. Dersom volatiliteten vurderes til å være for høy økes andelen risikofritt, og reduseres dersom den vurderes til å være for lav. Samme prinsipp gjelder også for halerisiko-mål, slik som VaR.
Den økonomiske gevinsten ved stabilisering av volatilitet er undersøkt av flere. Fleming et al. (2001), Fleming et al. (2003), Han (2005), Kirby og Ostdiek (2012) og Taylor (2014) har undersøkt porteføljer sammensatt av flere risikable aktiva, mens Marquering og Verbeek (2004), Moreira og Muir (2017), Bollerslev et al. (2018) og Dreyer og Hubrich (2019) har undersøkt porteføljer bestående av enkeltaktiva. De finner at det er økonomiske gevinster å hente ved styre volatiliteten sammenlignet med styring etter forventet avkastning. Videre finner Dreyer and Hubrich (2019) at nytten ved denne metoden først og fremst skriver seg fra en reduksjon av risikoen i venstrehalen på avkastningens sannsynlighetsfordeling, hvilket i seg selv er et argument for halerisiko-mål.
Funn av økonomisk gevinst ved volatilitetsmål er konsistent med tidligere funn som viser at såkalte minimumvarians-porteføljer (MVP) i gjennomsnitt gir et bedre avkastnings-risikoforhold («Sharpe’s Ratio») sammenlignet med annen porteføljeoptimering, se f.eks. Haugen og Baker (1991), Clarke et al (2006), Jagannathan og Ma (2003) og Scherer (2010). For norske forhold bekreftes disse resultatene i Lauvsnes (2018), hvor det vises at en MVP med 5 utvalgte sektorindekser i gjennomsnitt gjør det bedre enn hovedindeksen over tid. I sistnevnte artikkel underbygges resultatet med at siden «forventet avkastning hevdes å være mer ustabil enn varians-kovariansmatrisen, vil MVP være mer stabil og dermed lettere å predikere» (s. 229). Det vises blant annet til Jorion (1985), som hevder at forventet avkastning er ustabil og vanskeligere å predikere enn varians, hvilket gjør porteføljevektene ustabile når man optimerer ved maksimering av Sharpe’s ratio.
Men hva bør man velge å stabilisere, volatilitetsrisiko eller halerisiko? Bollerslev og Todorov (2011, s. 2187) finner at investorer frykter halerisiko mye mer enn volatilitetsrisiko, et fenomen de kaller «crash-o-phobia». De støtter således tidligere funn av Lee og Rao (1988), som finner at halerisiko bekymrer investorer mer enn volatilitet, men også at styring av volatilitet er effektivt kun dersom avkastningen følger en symmetrisk fordeling (se også Szegö (2002) og Strub (2013)). De empiriske funn indikerer nettopp mangel på symmetri – det er ikke tilstrekkelig for å unngå katastrofale tap å kun kontrollere porteføljens volatilitet. En rimelig tilnærming til forskningsspørsmålet i innledningen synes derfor å være en modell for kontroll av halerisiko under betingelsen av at momentene i avkastningsfordelingen skifter.
Introduksjon til modellen for stabilisering av halerisiko
Som et grunnlag for senere beregninger gjennomgås først prinsippene for beregning av VaR7. Deretter vises hvordan man kan benytte dette rammeverket til å bygge en enkel modell for stabilisering av halerisiko når momentene i avkastningsfordelingen er tilstandsavhengige.
Normal VaR for et enkeltaktivum
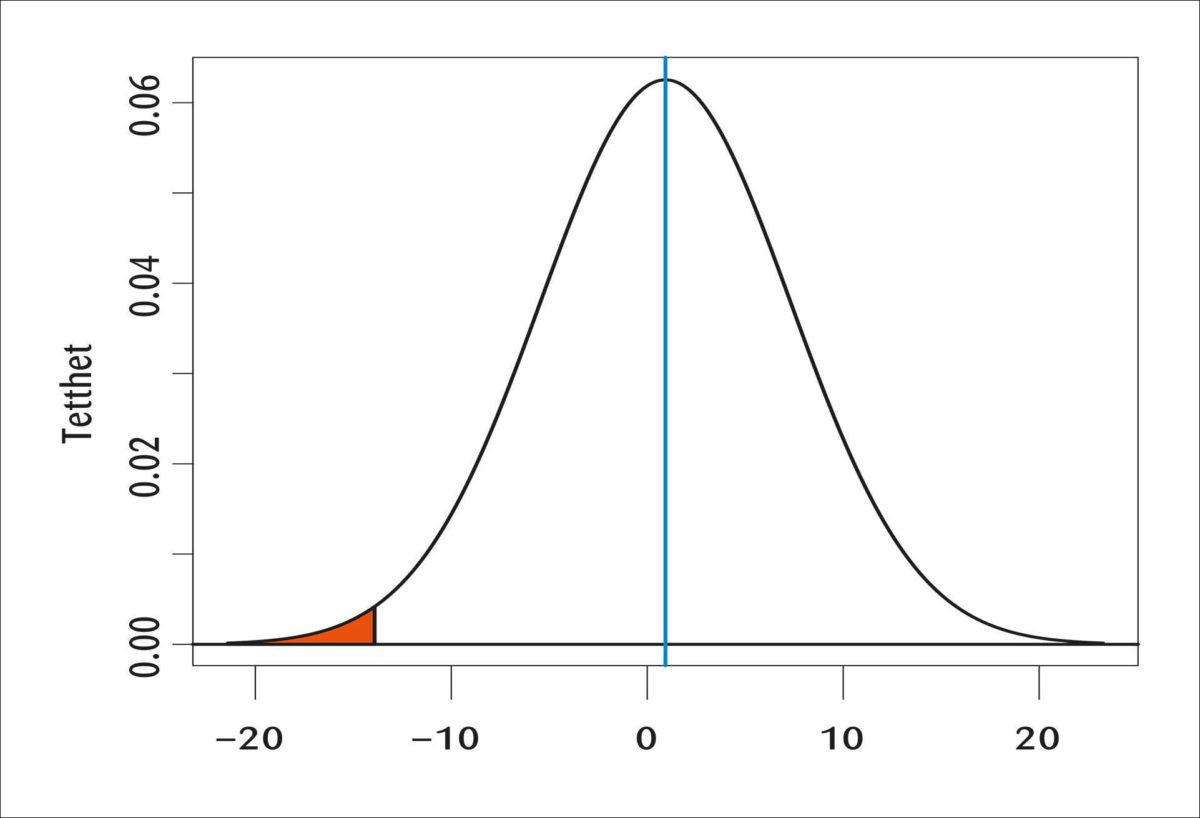
VaR er et statistikkbasert estimat på hvor stort et potensielt tap kan bli gitt en tidshorisont og et konfidensnivå (risikotoleranse). Formelt uttrykkes VaR som en betinget sannsynlighet , som leses: «sannsynligheten for at porteføljeavkastningen over m perioder er mindre enn eller lik alfa-kvantilen ». Denne kvantilen ligger i venstrehalen på den sannsynlighetsfordelingen man antar at avkastningen følger, og som det da er 1 − α prosent sannsynlig at avkastningen er bedre enn. Typisk settes α til 5 % (1 %). Dette betyr at Pr (Rm≤ Rα) =α, og man er da 95 % (99 %) sikker på at avkastningen i porteføljen er bedre enn Rα). Figur 1 viser at 99 % av tiden (dvs. α= 1%, se arealet farget rødt i venstre hale) er månedsavkastningen for hovedindeksen på Oslo Børs bedre enn (markert med grønn loddrett linje i figuren) dersom man antar at avkastningen er normalfordelt. Men denne antakelsen kan, som vi har sett fra de empiriske funn, være villedende.
For å illustrere konseptet Value at Risk (VaR) på enklest mulige måte skal vi anta at avkastningen til et finansielt verdipapir V er normalfordelt, med forventet (gjennomsnittlig) 6-månedlig avkastning og 6-månedlig standardavvik , dvs. . Den forenklende men feilaktige antakelsen om normalfordeling løses opp senere. Vi vil finne den verdien som gjør at 5%-kvantilen8 . Vi må da løse ut fra sannsynlighetsuttrykket . Det kan være nyttig for den kommende modellen å repetere beregningen av sannsynligheten for at en tilfeldig (stokastisk) variabel X er mindre enn eller lik en gitt verdi x, dvs. . Ved en standard normal transformasjon, , og uttrykt i vår notasjon får vi:
,4)
hvor er en standard normalfordelt variabel med gjennomsnitt lik 0 og standardavvik (og varians) lik 1. Dersom halesannsynligheten α=0,05 finner vi i en tabell eller et statistikkprogram at , =−1,645. Vi kan da sette inn for den kritiske kvantilen , og , og løse ut den tilsvarende kritiske kvantilen fra uttrykket
, 5)
som gir − , slik at , dvs. ca. −11,5%. Et generelt uttrykk for VaR i en normalfordeling blir da#Rα er typisk et negativt tall, mens VaR vanligvis oppgis som et positivt tall. I så fall blir uttrykket Rα= E(Rm) + Z · σ = -VaR.:
VaR 6)
Dersom investeringsbeløpet blir et tap lik om en måned lik 10000 ∙ (−0,115) =−1150. Verdien W1 etter en måned av investeringen gitt dette tapet blir:
kroner. 7)
Dersom vi setter blir , slik at VaR blir ca. −0,183%, dvs. ca. 1830 kroner. ville da blitt ca. 8170 kroner.
Value at Risk for portefølje av risikabelt og risikofritt aktivum
Poenget vårt er å vanne ut risikoen dersom verdien av VaR er for høy i en portefølje, ved å blande inn en andel av et risikofritt aktivum. For eksempel, anta at en småsparer ønsker å sette sammen en portefølje bestående av en andel i det risikable verdipapiret V og en andel i en sparekonto i banken til en gitt rente . Bankinnskudd inntil kr 2 millioner omfattes av den norske innskuddsgarantien, og kan anses som en risikofri investering. For øvrig kan kjøp av statsobligasjoner, dvs. utlån til den norske stat, også anses som risikofritt i den forstand at en er sikret mot konkurs, samt at en garanteres pålydende rente. Imidlertid er man ikke sikret mot markedsrisiko om man har bundet renten for en periode, pga. at renten på andre (nyere) verdipapirer kan gi bedre avkastning. La 6-måneders Rf =2%. Både forventet avkastning og standardavvik for porteføljen P blir avhengige av v:
8)
Standardavviket beregnes som kvadratroten av variansen til porteføljen ( ):
,
siden variansen til risikofritt aktivum, , og kovariansen mellom risikabelt og risikofritt aktivum, , pr. definisjon er lik null. Vi kan nå beregne VaR for porteføljen med samme metode som ovenfor:
9)
Dersom vi har en likevektet portefølje, dvs. v=0,5, blir VaR med våre data lik . Porteføljens halvårlige standardavvik og forventede avkastning blir hhv. 5,0 % og 3,5 %.
Kritisk tapsverdi – en modell for kontroll av halerisiko
Poenget med begrepet kritisk tapsverdi er som nevnt å sette et tak på porteføljens tapspotensial gitt investorens (eller myndighetenes) grad av risikoaversjon målt ved kvantil-sannsynligheten α. Når KTV og α er satt må man regne ut porteføljevektene for hhv. risikabelt og risikofritt aktivum.
Et praktisk eksempel med normalfordeling
Igjen bruker vi den forenklende forutsetningen om normalfordeling, slik at vi kan å fokusere på det generelle prinsippet på enklest mulig måte. Dette eksemplet er inspirert av Ruppert og Matteson (2015, s. 466), som benytter normalfordelingen i sitt eksempel. Vi antar at investoren setter α=0,01. Gitt må vi beregne hvor stor andelen v i det risikable aktivum V kan være. Vi setter KTV slik at i formel 9 for VaR, og løser for v.
, 10)
Vi finner at , og videre at . Andelen i risikofritt aktivum blir dermed 0,16. Standardavvik og forventet avkastning på denne porteføljen blir hhv. 8,40% og 4,52%.
Normal blandingsfordeling
Vi erstatter nå den forenklende forutsetningen om normalfordelt avkastning med den mer realistiske forutsetning om at avkastningen er sammensatt av to ulike fordelinger som hver representerer henholdsvis optimistisk og pessimistisk markedssentiment. Resultantfordelingen er en bivariat normal blandingsfordeling (BNBF), og vi utleder denne først før vi viser hvordan vi beregner sannsynligheter og finner andelen v i en BNBF.
Definisjon: bivariat normal blandingsfordeling
En normal blandingsfordeling representert ved en tetthetsfunksjon er en sannsynlighetsvektet sum av N andre normale tetthetsfunksjonerfor i=1,2,…,N. Vi skal kun se på tilfellet der N=2, dvs. en BNBF. Komponentfordeling representerer et optimistisk sentiment som gir en vekstfase (tilstand 1). Komponentfordeling representerer et pessimistisk sentiment, som gir en kontraksjonsfase (tilstand 2).
La betegne den langsiktige, ubetingede (også kalt ergodiske) sannsynligheten for forekomsten av et tilstand 1, mens er tilsvarende sannsynlighet for tilstand 2. Da har vi at avkastningen følger en BNBF som er et sannsynlighetsveid gjennomsnitt av to normale komponent-tetthetsfunksjoner og , jfr. ligning 11.
11)
Hver komponentfunksjon er gitt ved den normale tetthetsfunksjonen f(yit) i ligning 12:
12)
.jpg)
Figur 2
: Bivariat normal blandingsfordeling (BNBF) for OSEAX, 1990:10 – 2010:10.
Kilde: TITLON database, egne beregninger.
Merk forskjellen på konstanten i formel 12, og den ergodiske sannsynligheten π som angir vekten av hver komponentfordeling i resultantfordelingen . I tilstand 1 har avkastningen gjennomsnitt lik μ1 og standardavvik lik σ1, mens tilstand 2 har gjennomsnitt lik og standardavvik lik . Typisk er og , mens . Dersom tilstandene er vedvarende («persistente») vil akkumuleres til en stigende pristrend, og akkumuleres til en fallende pristrend9. Figur 2 og 3 viser disse fordelingene for Oslo Børs og S&P500. Legg merke til at den estimerte blandingsfordelingen (empirisk fordeling, blå) fanger opp den lange venstrehalen som karakteriserer aksjeavkastning. Legg også merke til stor varians og negativ forventningsverdi i pessimistisk tilstand (grønn) sammenlignet med optimistisk tilstand (rød). Den høyere volatiliteten i tilstand 2 (som impliserer større usikkerhet) forårsaker det vi observerer som opphopning av volatilitet («volatility clustering»). For aksjeindeksen OSEAX (som inneholder alle aksjer) på Oslo Børs er månedlige tilstandsavhengige karakteristika (avrundet) i perioden 1990:10 – 2010:10 estimert10 til , , og . De langsiktige sannsynlighetene for tilstand 1 eller 2 er beregnet til henholdsvis (ca.) og , hvilket betyr at i gjennomsnitt er vekstfaser i det norske markedet ca. 4 ganger mer sannsynlig enn kontraksjonsfaser. For den amerikanske referanseindeksen Standard & Poor 500 (S&P500) i perioden 1990:01 – 2014:04 er fordelingen beregnet til (ca.) , og Her er månedlige forventningsverdier henholdsvis 0,034 og -0,014, mens standardavvikene er henholdsvis 0,036 og 0,124. En tilsvarende BNBF for den amerikanske referanseindeksen S&P500 er gitt i figur 3.
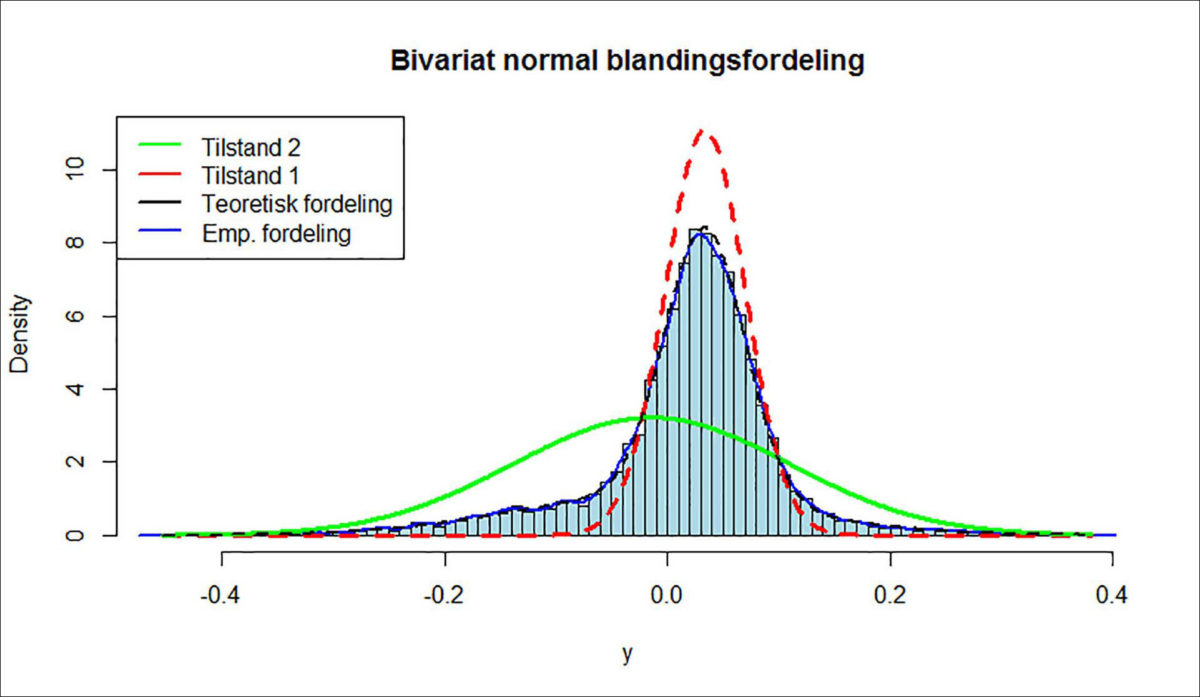
Kilde: FRED database, egne beregninger.
Sannsynlighetsberegning for KTV i en BNBF
Vi bruker samme forutsetning som i caset ovenfor, hvor vi antar at investoren setter en tapsgrense KTV = 15 % av investeringsverdien. Vi spør da: Hva er sannsynligheten for at tapet blir (dvs. at ) gitt at investeringens avkastning følger en BNBF? Dette kan regnes ut ved å stille opp en modell for betinget sannsynlighet. La hendelsen A betegne tilstand 1 slik at komplementet betegner tilstand 2. Definér , dvs. at tapet blir større enn eller lik terskelverdien KTV på −15%. Sannsynligheten for , , er et vektet snitt av de betingede sannsynlighetene i hver tilstand, og kan beregnes ut fra den første raden i matrisesystemet i ligning 13, jfr. Bayes teorem for betingede sannsynligheter:
13)
hvor betyr sannsynligheten for at avkastningen er bedre enn −15 %, jfr. konfidensnivået til høyre for Value at Risk- eller KTV-kvantilen. Vi får:
, 14)
som leses: sannsynligheten for større tap enn er lik sannsynligheten for et slikt tap gitt tilstand 1 multiplisert med sannsynligheten for tilstand 1, pluss sannsynligheten for et slikt tap gitt tilstand 2 multiplisert med sannsynligheten for tilstand 2. Dette kan også skrives , hvor betyr snitt og betyr union. Merk at er en halesannsynlighet på lik linje med .
.jpg)
Figur 4: Horisontal akse: . Vertikal akse: som funksjon av v.
Merknad
Hendelsen B kan inntreffe når hendelsen A inntreffer eller når hendelsen inntreffer. Dermed er Pr(B) et sannsynlighetsvektet gjennomsnitt av de to hendelsene og , og som representerer en kvantil i blandingsfordelingen. En konsekvens er at en blandingsfordeling med ergodiske sannsynligheter kan betraktes som en hypotetisk gjennomsnittlig ensemble-fordeling (en teoretisk uobserverbar tverrsnittsfordeling) for porteføljeavkastningen på ethvert tidspunkt t.
De betingede sannsynlighetene i utsagnet er gitt ved
, 15)
16)
hvor Z er en uavhengig standard normalfordelt variabel med varians lik 1 og gjennomsnitt lik 0. Dersom vi bruker tallene fra S&P500 ogr* =−0,15 får vi
. 17)
. 18)
Når vi multipliserer de betingede sannsynlighetene og med de respektive ergodiske sannsynlighetene 0,67 og 0,33, får vi den vektede sannsynligheten for tapshendelse B:
19)
Merk at sannsynligheten for hendelsen B, dvs. tap minst lik 15% gitt sannsynlighetsfordelingen i det optimistiske markedssentimentet i den ekspansive tilstand 1, er tilnærmet lik null . Gitt den pessimistiske og kontraktive tilstand 2 derimot, er denne sannsynligheten nokså høy, hele 13,57%. Dette illustrerer tydelig hvor viktig det er å bruke sannsynlighetsfordelinger som gjenspeiler den reelle risikoen.
Vi kan tolke resultatet av beregningen slik. Dersom investorens risikotoleranse var (dvs. konfidensnivå lik ville investeringen bli akseptert, siden . Det kan vises at den forventede VaR tilsvarende med disse dataene er ca. . Dersom risikotoleransen derimot var ville tilsvarende tapsverdi være 24,59%, og investeringsplanen ville dermed blitt kansellert. Anta så at økonomien befant seg i tilstand 2, dvs. . Halesannsynligheten i en BNBF for worst-case-tapet på 15%, ville da blitt 13,57%, som er ca. 2,7 ganger kravet . Dette illustrerer effekten av ikke å hensynta markedets tilstandsavhengighet i risikovurderingen. Dersom man brukte et datasett fra en relativt kort periode og som er karakterisert av tilstand 1, ville man underestimere den reelle risikoen grovt. Man bør derfor tilstrebe lange datasett som strekker seg over flere sykluser, og man bør kalkulere inn forekomsten av tilstand 2, dvs. finansverdenens «sorte svaner».
Optimal risikoreduksjon gitt konfidenskrav
Dersom KTV har for høy risiko, slik som tilfellet var for i blandingsfordelingen, eller ved i fordelingen til tilstand 2, kan man vanne ut porteføljevariansen ved å ta inn et risikofritt aktivum på samme måte som vist ovenfor. Derfor skal vi utvikle en metode for dette gitt at avkastningen følger en BNBF. Vi må først definere uttrykk for den samlede porteføljens avkastning , og standardavvik . Uten tilstandsavhengighet har vi sett at en portefølje bestående av en andel v av et risikabelt aktivum med avkastning lik og en andel av et risikofritt aktivum med avkastning lik gir forventet avkastning og standardavvik som dølger:
20)
21)
Forventet avkastning benevnes . I en BNBF erstattes standardavvik og forventning med deres respektive tilstandsavhengige momenter og , hvor . Hvis vi setter rf lik null for enkelhets skyld, hvilket også er realistisk i skrivende stund, kan de betingede sannsynlighetene for hendelsen B kan for hver tilstand i skrives som
, 22)
23)
Merk at og . Den gjennomsnittlige sannsynligheten for er uttrykkes ved de ergodiske sannsynlighetene slik:
24)
For en gitt risikotoleranse (dvs. halesannsynlighet) setter vi , og , slik at ligning 24 forenklet kan skrives som
25)
Vi skal imidlertid finne den optimale andelen v som gjør at porteføljen tilfredsstiller et gitt krav til risikotoleranse, og må løse ut v fra denne ligningen. Det finnes ingen analytisk løsning, og vi kan dermed ikke invertere funksjonen med hensyn på v slik som vist i eksemplet med normalfordelte data. Men vi kan løse problemet numerisk med et optimeringsverktøy, og finne den optimale verdien av v direkte#. I appendikset er det vist hvordan optimal v kan beregnes med problemløseren i Microsoft Excel. Fra figur 4 ser vi at optimal andel risikabelt, v, gitt er tilnærmet lik .
Forventet månedlig avkastning for denne porteføljen, med satt lik 0, er
, 26)
slik at . Merk at innholdet i hakeparentesene angir forventet porteføljeavkastning i hhv. tilstand 1 og 2, der 0,61 er vekten av risikabelt aktivum, og 0,39 er vekten av risikofritt aktivum. De respektive tilstandsavhengige forventningsverdier vektes så med de ergodiske sannsynlighetene, 0,67 og 0,33.
NB11
Anvendelse knyttet til likviditetskravet i baselregelverket
Prinsippet med risikoreduksjon av finansielle porteføljer kan også anvendes i likviditetsstyring for banksektoren, jfr. Baselregelverket såkalte «Liquidity Coverage Ratio», LCR (se for eksempel Basel Committee on Banking Supervision, 2019 s. 1049). LCR er gitt ved følgende brøk:
.27)
h
Brøken forteller at banken må besitte tilstrekkelig likvide midler til å betjene «net cash outflow» over en 30 dagers periode med økonomisk turbulens. Typisk er slike perioder karakterisert ved store børsfall og pessimisme i markedet, dvs. det vi har kalt tilstand 2 (eller hendelsen Ac). Banken kan la telleren i brøken bestå av en handelsportefølje («markedsportefølje») satt sammen av en blanding av risikable og risikofrie aktiva. For å tilfredsstille kravet til LCR kan banken så sette en KTV. Banken bør da sette et tak på forventet tap – en KTV – på sin markedsportefølje gitt tilstand 2, slik at gitt krav til halesannsynligheten . Telleren i LCR kan da være lik , hvor gir KTV benevnt i kroner eller annen valuta, og slik at x/ gir KTV benevnt i prosent når denne er forhåndsbestemt til å være .
Dermed sikrer banken seg – med et konfidensnivå gitt ved Baselregelverket12 – at likviditeten i markedsporteføljen står seg mot et worst case-scenario gitt ved Baselregelverket, og man vil kunne benytte verdiene i markedsporteføljen til å betjene forpliktelser dersom et worst case-scenario skulle inntreffe. Ved kun å bruke fordelingen for tilstand 2 når denne er estimert forenkles også beregningene, siden kun normalfordelingen benyttes. Det vil si at man kan benytte fremgangsmåten i seksjon 3.1, hvor optimal vekt v i risikabelt aktivum gitt risikotoleranse kan beregnes analogt med ligning 9 gitt tilstand 2, også benevnt . Dette gir , hvor både og er funksjoner av vekten i det risikable aktivum, v.
Oppsummering
- KTV tar utgangspunkt i et forhåndsbestemt maksimalt tap (kritisk tapsverdi) man ønsker å sikre seg mot. For eksempel, for en bank kan dette begrunnes med fremtidige forpliktelser og tilfredsstillelse av liquidity coverage ratio, og mer generelt med et ønske om å kontrollere nedsiderisikoen i en portefølje.
- Forskningen viser at stabilisering av halerisiko er en bedre måte å sikre seg mot store tap på enn volatilitetsstyring. Således kan KTV-metoden egne seg godt for aktiv forvaltning av oljefondet, og dermed oppnå en mer stabil utvikling av fondets verdi. Dette vil også kunne bidra til større politisk ro omkring forvaltningen av fondet, siden store tap i nedgangstider fremkaller uro og diskusjoner omkring forvaltningen. Stabiliseringen forutsetter at man benytter langsiktige modellparametere (ergodiske sannsynligheter, forventningsverdier og varians), og ikke forsøker å time disse. Investorens valgmuligheter er da risikotoleransen α og sammensetningen av den risikable porteføljen. Gitt disse parametere vil andelen risikofritt bestemmes av KTV og de ergodiske sannsynlighetene.
- KTV er en integrert metode hvor et «kapitalkrav» i form av likvide midler (dvs. risikofritt aktivum) beregnes simultant, og kan derfor være bedre egnet til likviditetsstyring. Metoden har også potensial til å kunne omfatte beregning av kapitalkrav generelt, hvor andelen av risikofritt aktivum er identisk med f.eks. et reservekrav eller krav til beholdning av kontanter og kontantekvivalenter.
Avsluttende bemerkninger
Artikkelens fokus er på risikoreduksjon for hindre oppbygging av finansielle ubalanser, som igjen kan føre til finanskriser. Det er rimelig å anta at dersom hypotesen om tilstandsavhengig avkastning ble gjort gjeldende i et regulatorisk rammeverk, ville man ha et virkemiddel mot utvikling av slike ubalanser forårsaket av underestimering av risiko og høy belåning i tilstand 1, og de realøkonomiske konsekvenser av dette som følger i tilstand 2.
Som et spesifikt bidrag er det vist hvordan man kan redusere risikoen i en portefølje under restriksjonene av en gitt maksimal (kritisk) tapsverdi og et gitt konfidensnivå, samt at porteføljens avkastning følger en bivariat normal blandingsfordeling med tilstandsavhengige parametere. Slike fordelinger er svært fleksible, og fanger opp viktige egenskaper ved empiriske fordelinger til finansiell avkastning, spesielt venstreskjevhet og tunge haler. En normal blandingsfordeling er også økonomiteoretisk attraktiv, siden skiftende sannsynlighetsfordelinger til finansielle aktiva kan overføres direkte til observerte vekslinger mellom optimistiske og pessimistiske markedssentiment. En forutsetter altså at data er trukket fra subpopulasjoner med hver sine karakteristiske parametere, og som bestemmes av skiftende markedsstemninger (sentiment). Vi har også estimert forventet avkastning og varians for begge tilstandene for norske og amerikanske aksjeindekser, og hvor hyppig hver enkelt forekommer i gjennomsnitt. I perioden 1990:10 – 2010:10 viser det seg at forventet avkastning skifter fra positiv til negativ i tilstand 2, og at variansen – dvs. usikkerheten – øker samtidig. I Norge forekommer tilstand 2 ca. 20 prosent av tiden, mens i USA ca. 33 prosent. I den grad disse sannsynlighetene og momentene er noenlunde stabile, må det dermed sies å være indikasjoner på en vesentlig risiko for ekstreme tap i begge markedene, og som KTV-modellen har potensial til å motvirke.
Artikkelen tar ikke for seg hvordan man skal sette sammen en optimal risikabelportefølje under samme betingelser med skiftende parametere. Dette vil være tema for fremtidig forskning. En viktig bestanddel i så måte vil være estimering av skiftende korrelasjoner.
Referanser
- Alexander, C. (2010). Value-at-Risk Models. John Wiley & Sons, Ltd. England.
- Ang, A. og Bekaert, G. (2002). International asset allocation with regime shifts. Review of Financial Studies, 15, 1137–1187.
- Ang, A. og Chen, J. (2002). Asymmetric correlations of equity portfolios. Journal of Financial Economics. Volume 63, Issue 3, March 2002, Pages 443–494.
- Bali, T. G., Mo, H. og Tang, Y. (2008). The role of autoregressive conditional skewness and kurtosis in the estimation of conditional var. Journal of Banking & Finance, 32(2), 269–282.
- Basel Committee on Banking Supervision (2011). Basel III: A global regulatory framework for more resilient banks and banking systems. Technical report, Bank for International Settlements.
- Basel Committee on Banking Supervision (2019a). The Basel Framework. Technical report, Bank for International Settlements. Draft.
- Basel Committee on Banking Supervision (2019b). Minimum capital requirements for market risk. Technical report, Bank for International Settlements, revised February 2019.
- Bollerslev, T., Hood, B., Huss, J. og Pedersen, L. H. (2018). Risk everywhere: Modeling and managing volatility. Review of Financial Studies, 31(7), 2729–2773.
- Bollerslev, T. og Todorov, V. (2011). Tails, fears, and risk premia. Journal of Finance, 66, 2165–2211.
- Butler, K.C og Joaquin, D.C (2002), Are the gains from international portfolio diversification exaggerated? The influence of downside risk in bear markets. Journal of International Money and Finance, 21, 981–1011.
- Campbell, J. Y. og Hentschel, L. (1992). No news is good news: An asymmetric model of changing volatility in stock returns. Journal of Financial Economics, 31, 281–318.
- Chabi-Yo, F., Ruenzi, S. og Weigert, F. (2018). Crash sensitivity and the cross section of expected stock returns. Journal of Financial and Quantitative Analysis, 53(3), 1059–1100.
- Clarke, R., H. De Silva og S. Thorley. (2006). Minimum-variance portfolios in the U.S. equity market. The Journal of Portfolio Management, 10–24.
- Cont, R. (2001). Empirical properties of asset returns: stylized facts and statistical issues. Quantitative Finance Volume 1, 223–236.
- Dreyer, A. A. og Hubrich, S. (2019). Tail-risk mitigation with managed volatility strategies. Journal of Investment Strategies, 8, 2956. 1.
- Fleming, J., Kirby, C. og Ostdiek, B. (2001). The economic value of volatility timing. Journal of Finance, 56, 329–352.
- Fleming, J., Kirby, C. og Ostdiek, B. (2003). The economic value of volatility timing using realized volatility. Journal of Financial Economics, 67, 473–509.
- Guidolin, M. og Timmermann, A. (2008). International asset allocation under regime switching, skew, and kurtosis preferences. Review of Financial Studies, 21, 889–935.
- Han, Y. (2005). Asset allocation with a high dimensional latent factor stochastic volatility model. Review of Financial Studies, 19(1), 237–271.
- Harvey, C. R. og Siddique, A. (1999). Autoregressive conditional skewness. Journal of Financial and Quantitative Analysis, 34, 465–487.
- Haugen, R. A. and N. Baker. (1991). The effcient market ineffciency of capitalization weighted stock portfolios. The Journal of Portfolio Management, 35–40.
- Jagannathan, R. og T. Ma. (2003). Why Imposing the Wrong Constraints Helps. The Journal of Finance, 58(4), 1651–1683.
- Jondeau, E. og Rockinger, M. (2003). Conditional volatility, skewness, and kurtosis: existence, persistence, and comovements. Journal of Economic Dynamics and Control, 27, 1699–1737.
- Jorion, P. (1985). International Portfolio Diversification with Estimation Risk. The Journal of Business, 58/3, s. 259–278.
- Kirby, C. og Ostdiek, B. (2012). Its all in the timing: simple active portfolio strategies that outperform naive diversification. Journal of Financial and Quantitative Analysis, 47, 437– 467.
- Knutsen, S. (2008). Finansielle kriser i aktuelt og historisk perspektiv. Magma, Fagpressen, Oslo.
- Lauvsnes, S. O. (2018). Er hovedindeksen en optimal portefølje med hensyn til avkastning og risiko? Praktisk Økonomi og Finans, 3, 226–238.
- Lee, W. Y. og Rao, R. K. (1988). Mean lower partial moment valuation and lognormally distributed returns. Management Science, 34, 446–453.
- Markowitz, H.M. (March 1952). Portfolio Selection. The Journal of Finance. 7 (1): 77–91.
- Mandelbrot, B. (1963) The variation of certain speculative prices. J. Business XXXVI 392–417.
- Marquering, W. and Verbeek, M. (2004). The economic value of predicting stock index returns and volatility. Journal of Financial and Quantitative Analysis, 39, 407–429.
- Moreira, A. og Muir, T. (2017). Volatility-managed portfolios. Journal of Finance, 72, 1611– 1644.
- Regjeringen (2011). Bedre rustet mot kriser – Finanskriseutvalgets utredning. NOU 2001:1. Tilgjengelig på https://www.regjeringen.no/no/dokumenter/nou-2011-1/id631151/?ch=4
- Ruppert, D. og Matteson, D.S. (2015). Statistics and Data Analysis for Financial Engineering. Springer.
- Rydén, T., Teräsvirta, T. og Åsbrink, S. (1998). Stylized facts of daily return series and the hidden Markov model. Journal of Applied Economics, 13, 217–244.
- Schaller, H. og Van Norden, S. (1997). Regime switching in stock market returns. Applied Financial Economics, ss. 177–191.
- Scherer, B. 2010. A New Look at Minimum Variance Investing. Tilgjengelig på SSRN: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1681306
- Strub, I. S. (2013). Tail hedging strategies. Tilgjengelig på https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2261831 .
- Szegö, G. (2002). Measures of risk. Journal of Banking & Finance, 26(7), 1253–1272.
- Taylor, N. (2014). The economic value of volatility forecasts: A conditional approach. Journal of Financial Econometrics, 12, 433–478.
Vedlegg: Beregning av optimal andel av risikofritt aktivum
Finn optimal andel risikabelt (benevnt v) ved hjelp av Solver i Excel når alfa = 0,01:
.jpg)
Figur A1: Skjermbilde fra regneark i Microsoft Excel.
Formel i celle B10 er sannsynligheten , jfr. ligning 22: =NORMALFORDELING(B2;B13*B3;B13*B5;SANN (Excel returnerer en feilmelding)
Formel i celle B11 er sannsynligheten , jfr. ligning 23:: =NORMALFORDELING(B2;B13*B4;B13*B6;SANN)
Sett inn en startverdi i for v i celle B13, f.eks. 0,5.
Formel i celle B14 (ligning 24) settes lik null: =B7*B10+B8*B11-0,01
En kan også definere alfa som en parameter, slik at formelen i celle B14 blir : =B7*B10+B8*B11-alfa hvor alfa = .
-
Spesifiser i problemsløseren (solver), se figuren nedenfor:
Åpne problemsløseren fra Data/Problemløser.
Definer hvilken celle som skal endres (B13).
Definer begrensninger, som er verdimengden for v. Nedre grense bør settes > null
-
Klikk «Løs». Dersom en løsning eksisterer, endres celle B13 slik at celle B14 blir (tilnærmet) lik 0.
.jpg)
Figur A2: Skjermbilde «problemløser» (solver) i Microsoft Excel.
Fotnoter:
- E-post: svein.o.lauvsnes@nord.no. ↩︎
- Se f.eks. Regjeringen (2011) og Knutsen (2008). ↩︎
- Se f.eks. Ang og Bekaert (2002), Ang og Chen (2002), Butler og Joaquin (2002), Guidolin og Timmerman (2008). ↩︎
- Den norske oversettelsen av skriftstedet er ikke spesielt opplysende, derfor gjengis den engelske: «But divide your investments among many places, for you do not know what risks might lie ahead». ↩︎
- Volatilitet er det samme som standardavviket til avkastningen, beregnet som kvadatroten av variansen. Dette er et risikomål som er lettere tolke enn variansen siden sistnevnte er gjennomsnittlig kvadrert avvik fra forventet avkastning, mens standardavviket har samme benevning som avkastningen. ↩︎
- Venstreskjevhet vil si at det er større sannsynlighet for ekstreme tap (negativ avkastning) enn det normalfordelingen gir. ↩︎
- Fremstillingen av parametrisk normal VaR i denne seksjonen er delvis basert på Alexander (2008), men også på egenproduserte eksempler som har blitt brukt i undervisning. ↩︎
- For å gjøre notasjonen enklest mulig undertrykker vi fotskriften Rα, og skriver Rα i stedet for Rm,α. ↩︎
- Det at forventet avkastning kan skifte fortegn kan forklare hvorfor porteføljeoptimering ved maksimering av Sharpe’s ratio fungerer dårligere enn minimumvarians-porteføljen. ↩︎
- Med programvaren R og pakken depmixs4. Programmeringskoder kan fås ved henvendelse til forfatteren. ↩︎
- Programmering i statistikkverktøyet R gir v(α = 0,01) = 0,6100. R-script som viser alle utregninger og grafer er tilgjengelig ved henvendelse til forfatteren. ↩︎
- I Baselregelverket er VaR erstattet med betinget VaR, dvs. halerisikoen skal angis med gjennomsnittet av utfallene utover VaR-kvantilen (kalt Conditional VaR eller CVaR). I normalfordelingen er dette enkelt å beregne. ↩︎
