Handlingsregelen sikrer ikke realverdien av oljefondet og gir uforutsigbar finanspolitikk
Denne artikkelen viser hvorfor handlingsregelen ikke sikrer verdien av oljefondet for fremtidige generasjoner slik det blir hevdet. Jeg simulerer verdien av oljefondet i 100 år med en empirisk fordeling av avkastningen av oljefondet. Et optimistisk anslag på medianverdien av oljefondet om 100 år er 64 prosent av dagens verdi dersom vi følger handlingsregelen. Handlingsregelen fører også til en uforutsigbar finanspolitikk. Alternative finanspolitiske regler som gir en stabil finanspolitikk, kan føre til at oljefondet tømmes raskere. En viktig politisk avveining er mellom stabilitet i finanspolitikken og stabilitet i verdien av oljefondet.
Handlingsregelen sikrer ikke realverdien av oljefondet og gir uforutsigbar finanspolitikk1
Innledning
Da Nicolai Tangen under et besøk på NHH i fjor høst ble spurt om hvor lenge oljefondet kan vare, svarte Tangen: «Dette er ren matematikk. Fondets levetid avhenger av hvor mye vi putter inn, hvilken avkastning vi får og hvor mye vi tar ut.»2 Dette er selvsagt riktig, men hvor mye vi tar ut styres jo av handlingsregelen med hensikt på å spare oljeinntektene for fremtidige generasjoner. Meld. St. 29 (2000–2001) som etablerte handlingsregelen, slår fast at «En politikk basert på å bruke forventet realavkastning av Petroleumsfondet sikrer at realverdien av fondet ikke reduseres.» Coiner (1990) har derimot vist at dersom man bruker den forventede avkastningen av en formue vil den over tid brukes opp.3 Likevel gjentas påstanden nærmest som et mantra og det er en utbredt oppfatning om at den er sann. Påstanden bygger imidlertid på feil bruk av de store talls lov. Denne artikkelen fyller dermed et behov for å opplyse om og forklare hvorfor handlingsregelen ikke sikrer realverdien av oljefondet, men i stedet fører til at vi bruker den opp.
Med en empirisk fordeling over avkastningen til oljefondet anslår jeg med simuleringer hvor mye av fondet vi har brukt opp om 100 år dersom vi følger handlingsregelen. Jeg viser også at dersom vi bruker 50 basispunkter mindre enn forventet avkastning er det mulig å bevare oljefondet for evigheten, men ikke med sikkerhet. Det gjør vi bare dersom vi bruker den faktiske avkastningen av oljefondet.
Den brede politiske oppslutningen om handlingsregelen har sammenheng med at oljeinntektene har fylt opp fondet som har gitt rom for en gradvis økning i bruk av oljepenger i økonomien. En heldig utvikling i finansmarkedene har bidratt til ytterligere vekst og sikret verdien av hovedstolen (se Wulfsberg, 2018). Betydelige oljeinntekter den nærmeste tiden vil øke handlingsrommet ytterligere, men om ikke lenge vil oljeinntektene avta. Da viser simuleringene i denne artikkelen at å bruke en fast andel av fondet innebærer en svært uforutsigbar finanspolitikk. Blant andre Kjelsrud (2018) og Henriksen (2022) har også påpekt at handlingsregelen gir stor variasjon i finanspolitikken. Dette er også påpekt av Rådgivende utvalg for finanspolitiske analyser (2022a) som foreslår å utrede alternativer til handlingsregelen blant annet en kontantstrømregel (se Holden, 2022). En finanspolitisk regel som gir en mer stabil finanspolitikk enn det handlingsregelen gjør vil imidlertid vil ha konsekvenser for levetiden til oljefondet. Dersom man ønsker å stabilisere bruken av oljepenger på dagens nivå kan oljefondet være tømt i løpet av en generasjon. Ved valg av finanspolitisk handlingsregel står altså politikere overfor en avveining mellom stabil finanspolitikk og bevaring av oljeformuen.
NOU (2016) simulerte verdien av oljefondet under ulike forutsetninger om aksjeandelen i porteføljen, men bare 30 år fram i tid. Dette er en svært kort horisont for å vurdere hvorvidt handlingsregelen sikrer oljefondets verdi over generasjoner. Dessuten inkluderer simuleringene tilførsel av oljeinntekter gjennom perioden som tilslører effekten av handlingsregelen på oljefondet. Disse simuleringene viser likevel at det er en ikke ubetydelig risiko for et fall i verdien av oljefondet til tross for at det tilføres nye oljeinntekter. Simuleringer i en analyse fra Rådgivende utvalg for finanspolitiske analyser (2022a og 2022b) er også bare over 30 år og inkluderer tilførsel av oljeinntekter. Mork mfl. (2022) ser bort fra fremtidige oljeinntekter og predikerer at oljefondets verdi kan være halvert 40 år fram i tid dersom vi følger handlingsregelen. Deres simuleringer tar også hensyn til effekter av stokastiske konjunkturer og motsyklisk finanspolitikk og valutakurseffekter. Denne artikkelen er enklere ved å rendyrke effekten av å bruke en fast andel av oljefondet over 100 år for å tydeliggjøre sammenhengen mellom handlingsregelen og levetiden til oljefondet.
Oljefondet og handlingsregelen
For å simulere verdien av oljefondet frem i tid må vi ta hensyn til den gjensidige sammenhengen mellom handlingsregelen og oljefondets verdi. Det er også nyttig med en begrepsavklaring. Oljefondets verdi i NOK ved utgangen av året Wt avhenger av avkastningen i NOK rt på fondets verdi ved inngangen til året, oljeinntekter Υt som overføres ubeskåret til oljefondet, og statsbudsjettets oljekorrigerte budsjettunderskudd Bt som finansieres med en overføring fra oljefondet:
(1)
Alle variabler er i faste priser i NOK med unntak av realavkastningen som er en rate.
Handlingsregelen sier at det strukturelle oljekorrigerte budsjettunderskuddet BtS skal over tid være lik forventet avkastning ρ av fondets verdi ved inngangen av året. Men handlingsregelen er fleksibel og tillater å avvike fra forventet avkastning dersom den økonomiske situasjonen tilsier en diskresjonær motsyklisk politikk eller for å glatte budsjettunderskuddene dersom oljefondets verdi varierer mye.4 Vi kan formulere handlingsregelen som
(2)
der fanger opp diskresjonære tiltak og glatting. Det oljekorrigerte budsjettunderskuddet kan dekomponeres i det strukturelle oljekorrigerte budsjettunderskuddet og en syklisk budsjettkomponent som representerer automatiske stabilisatorer, det vil si . Vi kan dermed kombinere oljefondets akkumuleringsidentitet (1) og handlingsregelen (2), slik at vi får en dynamisk ligning for utviklingen av oljefondets verdi:
(3)
Det første leddet sier at dersom den faktiske avkastningen er større enn forventningen vil verdien av oljefondet øke (siden vi bruker forventet avkastning). I tillegg kommer løpende oljeinntekter fratrukket kostnader ved motsyklisk konjunkturpolitikk ( ). Løsningen av den dynamiske ligningen (3) blir
(4)
der er rentes rente fra år 1 til år t, slik at er rentes rente fra år s+1 til t. Merk at rentes rente gjelder for ekstraavkastningen . Vi kan tolke ligningen historisk som at dagens verdi av oljefondet er rentes rente av akkumulerte oljeinntekter minus akkumulerte kostnader ved motsyklisk finanspolitikk (initialverdien til fondet var 0). Ser vi derimot fremover i tid vil oljefondets verdi avhenge av rentes rente av dagens fondsverdi pluss akkumulerte rentes rente av fremtidige oljeinntekter minus fremtidige kostnader ved motsyklisk konjunkturpolitikk.
Vi kan bruke (4) til å anslå verdien av oljefondet fremover. Men for å få fram betydningen av handlingsregelen skal vi se bort fra fremtidige oljeinntekter og motsyklisk konjunkturpolitikk, slik at for alle år fremover. Dette tilsvarer en forutsetning om at alle fremtidige storting vedtar budsjettunderskudd som følger handlingsregelen uten avvik. Samtidig ser vi bort fra effekten av konjunktursvingninger, slik at simuleringene kan tolkes som et optimistisk tilfelle. Når vi ser bort fra tilførsel av nye oljeinntekter får vi tydelig fram effekten av handlingsregelen på oljefondets verdi. Under disse forutsetningene er verdien av oljefondet dermed gitt av
(5)
(5) viser at verdien av oljefondet fremover er rentes rente av ekstraavkastningen av dagens verdi.
Ideen om at vi bevarer oljefondets verdi dersom vi bruker forventet avkastning bygger på de store talls lov: hvis vi av og til bruker litt mer enn den faktiske avkastningen og av og til litt mindre så vil vi over tid bruke gjennomsnittlig avkastning og dermed bevare oljefondets verdi (hvis vi av og til hugger litt mer av skogen enn den faktiske tilveksten og av og til litt mindre så vil vi over tid bevare skogen). Problemet med dette resonnementet er at de store talls lov gjelder kun for summer og ikke et produkt som i ligning (5). Verdien av fondet avhenger av rentes rente av ekstraavkastningen og ikke summen av ekstraavkastningen.
Coiner (1990) forklarte hvorfor (5) innebærer at fondets verdi forsvinner over tid og jeg gjentar forklaringen her. Hvis vi antar at realrenten er stokastisk og er uavhengig normalfordelt med forventning og standardavvik slik som i NOU (2016), da er rentes rente faktoren også normalfordelt, men med forventning lik 1 og standardavvik . Verdien av fondet vil da bli lognormalfordelt med forventning og standardavvik . Lognormalfordelingen har en lang hale for store verdier av fondet. I forventning vil fondets verdi bevares, men fordi variansen øker over tid vil medianen bli lavere og lavere og gå mot 0 i fremtiden og sannsynligheten for at fondets verdi blir 0 går mot 1. Med normalfordelt avkastning og et standardavvik på 10 prosent kan det vises at medianverdien av fondets verdi om 100 år er bare 60 prosent av fondets initiale verdi. I dette eksempelet har handlingsregelen altså medført at vi i medianverdi har brukt opp 40 prosent av fondets verdi ila 3–4 generasjoner. Et viktig poeng er at desto større variasjon i avkastningen jo raskere tømmes oljefondet.
Intuisjonen for dette resultatet er den samme som at man kommer dårligere ut dersom man først taper prosent og deretter vinner prosent (eller omvendt) av en formue. Anta at det bare er to perioder og at initialformuen er 1. I hver periode får man enten en rente på eller prosent med lik sannsynlighet. Har man vært heldig i begge periodene sitter man igjen med med sannsynlighet 0,25. Har man derimot vært uheldig begge periodene sitter man igjen med også med sannsynlighet 0,25. Hvis man er heldig i den ene perioden og uheldig i den andre sitter man igjen med med sannsynlighet 0,5. I dette eksempelet er forventningen lik 1, men medianen er altså mindre enn 1. Man kan enkelt utvide resonnementet med flere perioder til å vise at medianen vil falle over tid.
Oljefondet om hundre år
For å illustrere betydningen av handlingsregelen for oljefondets verdi, har jeg simulert verdien 100 år frem i tid med utgangspunkt i ligning (5). De stokastiske egenskapene ved avkastningsraten i forhold til bruken av oljepenger bestemmer verdien av oljefondet. Disse egenskapene avhenger blant annet av investeringsstrategien til oljefondet som var tema for NOU (2016). En høyere aksjeandel gir en høyere forventet avkastning, men også en høyere variasjon. Valutakursutviklingen vil også påvirke fordelingen til . I stedet for å anta at er normalfordelt skal jeg bruke en empirisk fordeling av som er konstruert ved å skrape verdien av oljefondet fra nbim.no en gang i timen fra april 2018 til september 2019. Basert på disse observasjonene simulerer jeg en fordeling av årlige avkastningsrater som har et standardavvik på 8,8 prosent og er svakt høyreskjev, se Carpena og Wulfsberg (2019) for detaljer. I tillegg normaliserer jeg fordelingen slik at . Til sammenligning legger NOU (2016) til grunn for sine simuleringer med 60 prosent aksjeandel, en normalfordeling med standardavvik på 11,9 prosent. Til tross for at aksjeandelen er økt til 70 prosent har altså den fordelingen som jeg bruker her, et standardavvik som er 3,1 prosentpoeng lavere enn i NOU (2016). Det er mulig at lavere variasjon skyldes at den simulerte fordelingen av årlig avkastning er basert på observasjoner over en forholdsvis kort periode. Likevel, ved å skrape dataene hver time kan man konstruere et rimelig bilde av variasjonen i den årlige avkastningen med en empirisk forankring. I simuleringene forutsetter jeg videre at den årlige avkastningen er stokastisk uavhengig over tid.
Figur 1 viser resultatet av 10.000 simuleringer av fondets verdi 100 år fram i tid der jeg har normalisert fondets verdi i dag til 1. Vi ser at gjennomsnittet holder seg nær initialverdien, at medianen faller og variasjonen øker over tid i tråd med Coiner (1990). Over tid ligger stadig mer av sannsynlighetsfordelingen under 1 som samsvarer med eksempelet med normalfordeling over. Etter 100 år er medianverdien bare 64 prosent av initialverdien og hele 70 prosent av utfallene er lavere enn 1 som betyr at oljefondet er blitt mindre enn ved utgangspunktet.
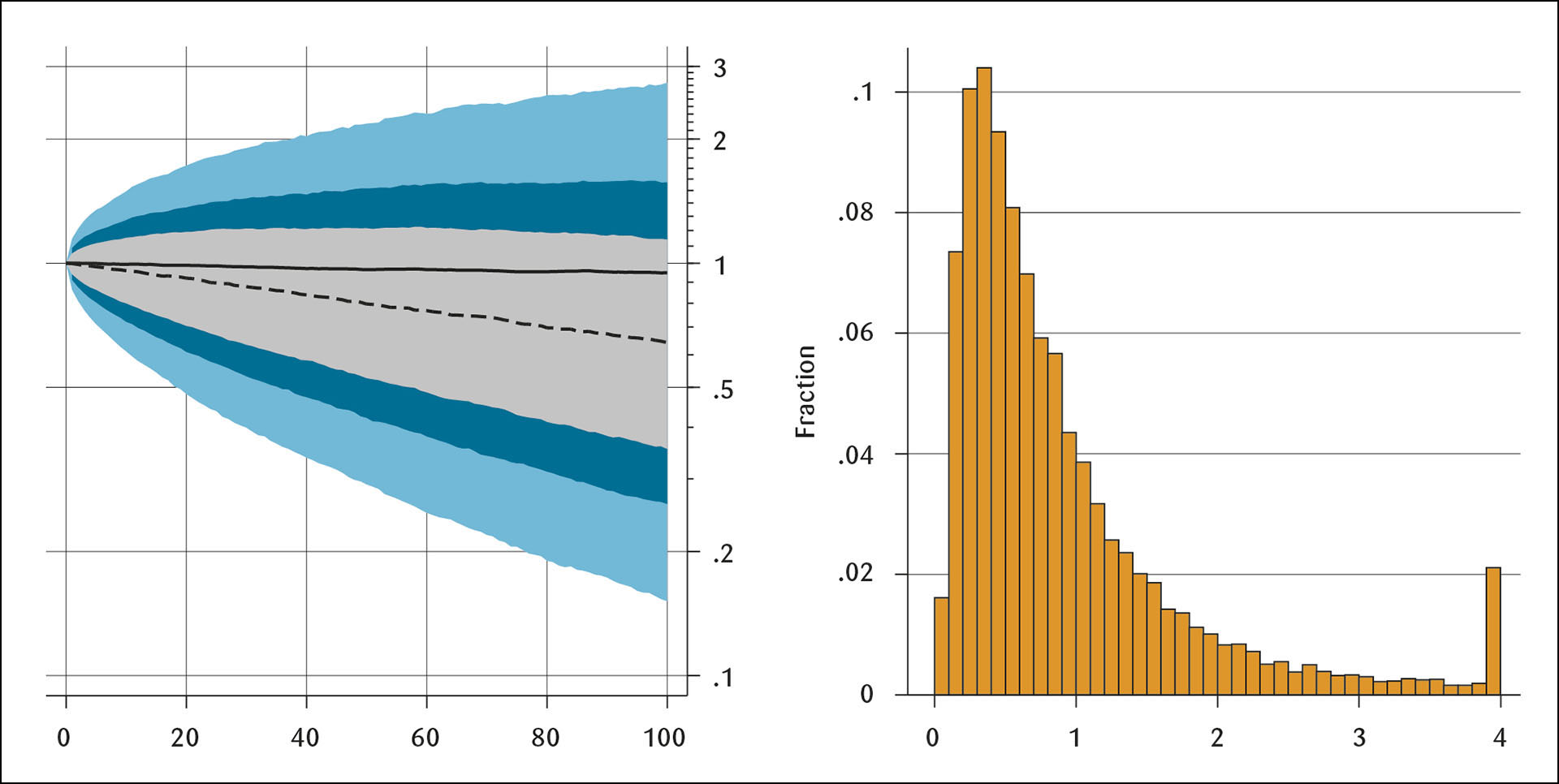
Figur 1
Venstre: Simulering av verdien til oljefondet med dagens handlingsregel 100 år frem i tid. Heltrukken linje viser gjennomsnittet, stiplet linje viser median, grått bånd viser 50%, blått bånd viser 70% og lyseblått bånd viser 90% usikkerhetsintervall. Logaritmisk skala. Høyre: Trunkert histogram av oljefondets verdi etter 100 år.
Histogrammet i Figur 1 illustrerer sannsynlighetsfordelingen til oljefondet etter 100 år og likner en lognormalfordeling. Ettersom tiden går, vil mer og mer av fordelingen nærme seg 0. Det er altså ingen grunn til å hevde at handlingsregelen sikrer oljefondets verdi, snarere tvert imot. Høyere variasjon i betyr et raskere fall i medianen (og fordelingen). Dette innebærer at valget av aksjeandelen i oljefondets portefølje ikke bare et valg mellom risiko og forventet avkastning, men også hvor fort vi tømmer oljefondet.
Simuleringene er som sagt basert på betydelig mindre varians i avkastningen i forhold til forutsetningene i NOU (2016). Dette tilsier at simuleringene trolig viser et mer optimistisk forløp for verdien av oljefondet. Det er også mulig at observasjoner av verdien av oljefondet over en lengre periode ville resultere i mer variasjon og dermed en raskere tapping av fondet.
Simuleringene forutsetter også at avkastningen er stokastisk uavhengig fra år til år. Dersom en høyere avkastning enn forventet skulle bli etterfulgt av lavere avkastning enn forventet året etter vil det redusere variasjonen. NOU (2016) anslår imidlertid at slik tilbakevending mot gjennomsnittet reduserer risikoen kun med to-tre prosent.
Det er mulig å motvirke tappingen av oljefondet ved å bruke mindre enn forventet avkastning. Ho mfl. (2010) viser at dersom man bruker mindre enn forventet avkastning unngår man at sannsynlighetsfordelingen for oljefondet går mot 0. For eksempel hvis unngår man dette med å bruke 2,5 prosent av oljefondet hvis forventet avkastning er 3 prosent ( ). Figur 2 viser simuleringer av verdien til oljefondet hvis vi bruker 2,5 prosent i stedet for 3 prosent med samme empirisk fordeling for .
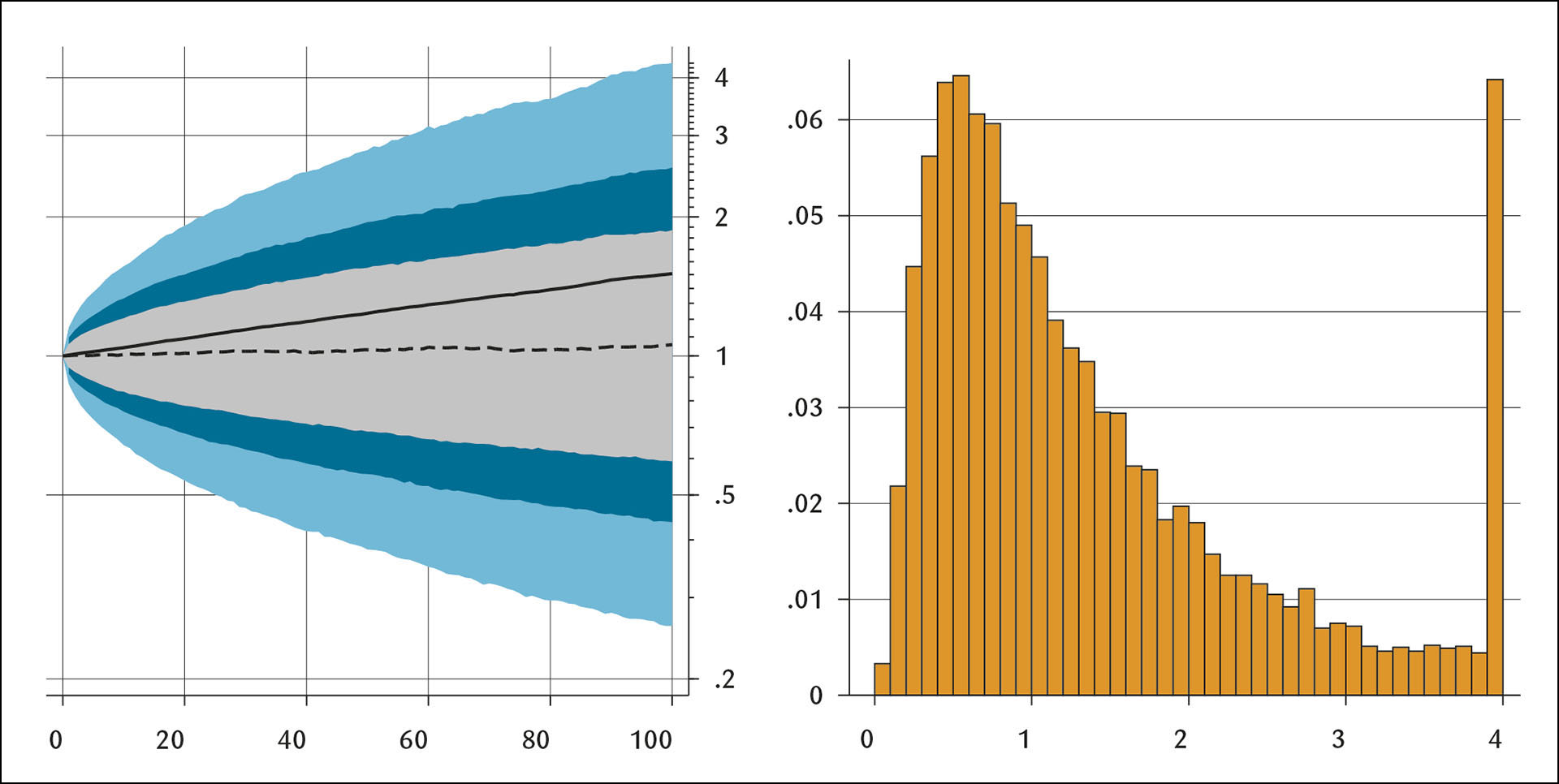
Figur 2
Venstre: Simulering av verdien til oljefondet med en handlingsregel der man bruker 2,5% av oljefondets verdi 100 år frem i tid. Heltrukken linje viser gjennomsnittet, stiplet linje viser median, grått bånd viser 50%, blått bånd viser 70% og lyseblått bånd viser 90% usikkerhetsintervall. Logaritmisk skala. Høyre: Trunkert histogram av oljefondets verdi etter 100 år.
Simuleringene i Figur 2 viser at medianen i dette tilfelle er stabil nær 1, mens gjennomsnittet vokser. Det er ingen tendens til at fordelingen konvergerer mot 0 som i Figur 1. En slik regel kan altså stabilisere verdien av oljefondet i betydningen at det er like sannsynlig at fondet blir større som at det blir mindre. Men heller ikke en slik regel vil sikre realverdien av oljefondet. I tillegg ser vi at variasjonen er betydelig høyere enn i Figur 1.
Ustabil finanspolitikk
Hvis man skal sikre at fondet bevarer sin verdi ser vi fra ligning (5) at løsningen er å bruke den faktiske avkastningen hvert år, men det vil jo medføre uakseptable svingninger i finanspolitikken. Men også handlingsregelen innebærer en betydelig variasjon i finanspolitikken som mange har påpekt (blant annet Henriksen, 2022, og Rådgivende utvalg for finanspolitiske analyser, 2022a og 2022b). Simuleringene i denne analysen viser dette tydelig. Figur 1 kan også tolkes som en illustrasjon av den variasjonen i det strukturelt oljekorrigerte budsjettunderskuddet som følger av handlingsregelen der initialverdien er normalisert til 1.5 Men Figur 1 viser kanskje ikke like tydelig hvor mye variasjon handlingsregelen innebærer for en gitt bane. Figur 3 viser eksempler på denne variasjonen med tre tilfeldige baner fra simuleringene med handlingsregelen. Det er en enorm forskjell mellom banene, men også betydelig variasjon for hver bane. Det er en underdrivelse å si at det krever en svært streng fiskal disiplin for å akseptere og holde seg til et gitt forløp for budsjettunderskuddene. Det kan også se ut som at politikere og folk flest ikke har erkjent denne uforutsigbarheten.
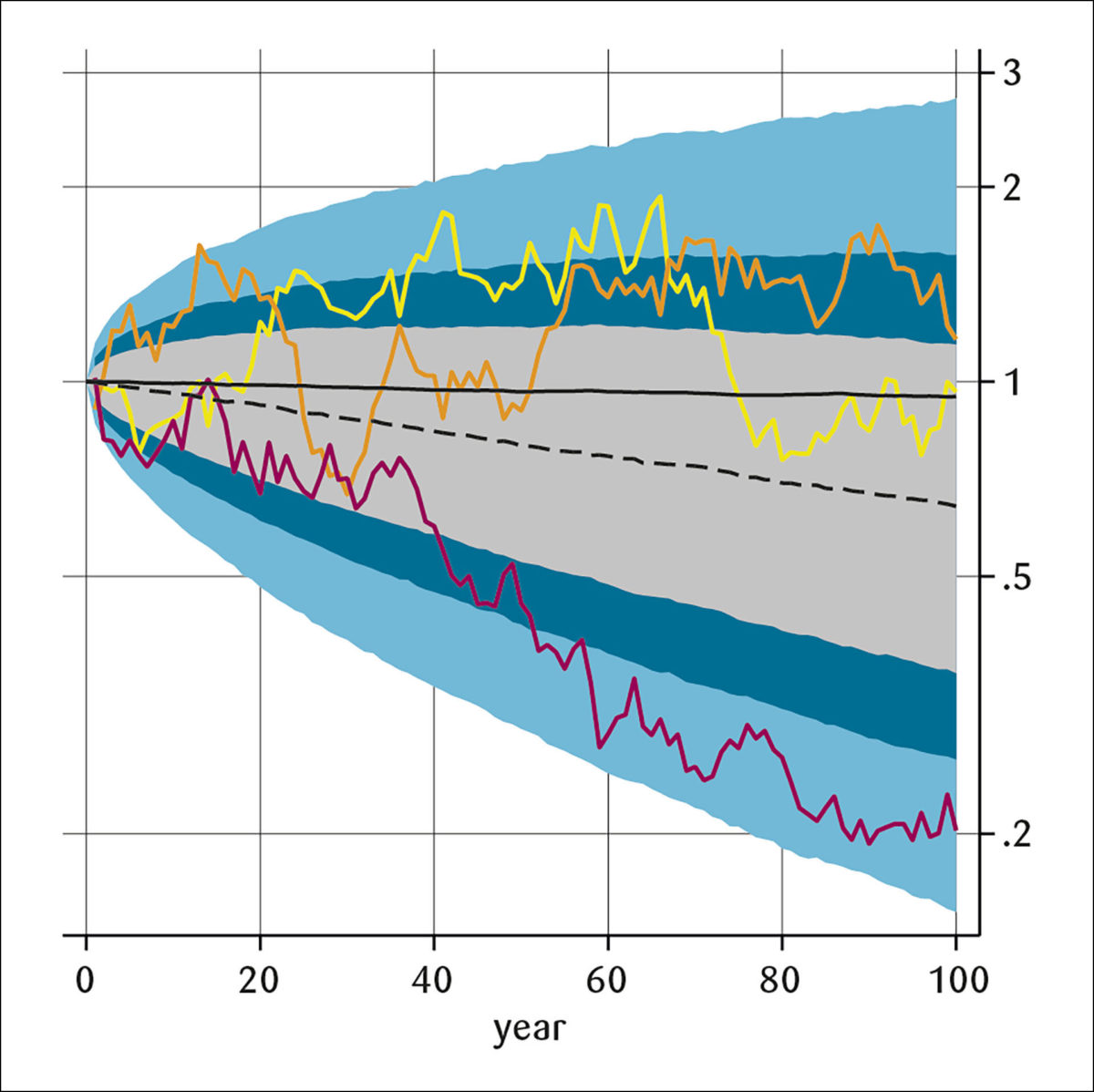
Tre tilfeldige baner for strukturelt oljekorrigert budsjettunderskudd lagt oppå Figur 1.
Betydelig variasjon i finanspolitikken (utover motsyklisk konjunkturpolitikk) er selvsagt ikke ønskelig. Derfor tar mange til orde for å endre handlingsregelen. Rådgivende utvalg for finanspolitiske analyser (2022) foreslår å utrede om budsjettunderskuddene i stedet bør knyttes til kontantstrømmen til oljefondet. Kontantstrømmen varierer mindre enn verdien av oljefondet slik at finanspolitikken blir mer stabil, se Holden (2022).
Et enklere alternativ vil være å ha en finanspolitisk regel med mål om et gitt budsjettunderskudd som andel BNP som mange andre land, og som er foreslått av blant andre Bjørnland (2022). En slik regel vil frakople finanspolitikken fra svingninger i oljefondet og gi helt forutsigbare og stabile rammer for finanspolitikken. Men å velge en mer stabil finanspolitisk regel vil selvsagt ha konsekvenser for verdiutviklingen av fondet. Et nærliggende eksempel er hvilke konsekvenser det har å fortsette med dagens nivå på budsjettunderskuddene. Med samme fremgangsmåte som over har jeg simulert oljefondet fremover, men der jeg erstatter handlingsregelen med en målsetting om at budsjettunderskuddet skal være 10 prosent av Fastlands BNP som jeg antar vokser med 2 prosent per år.
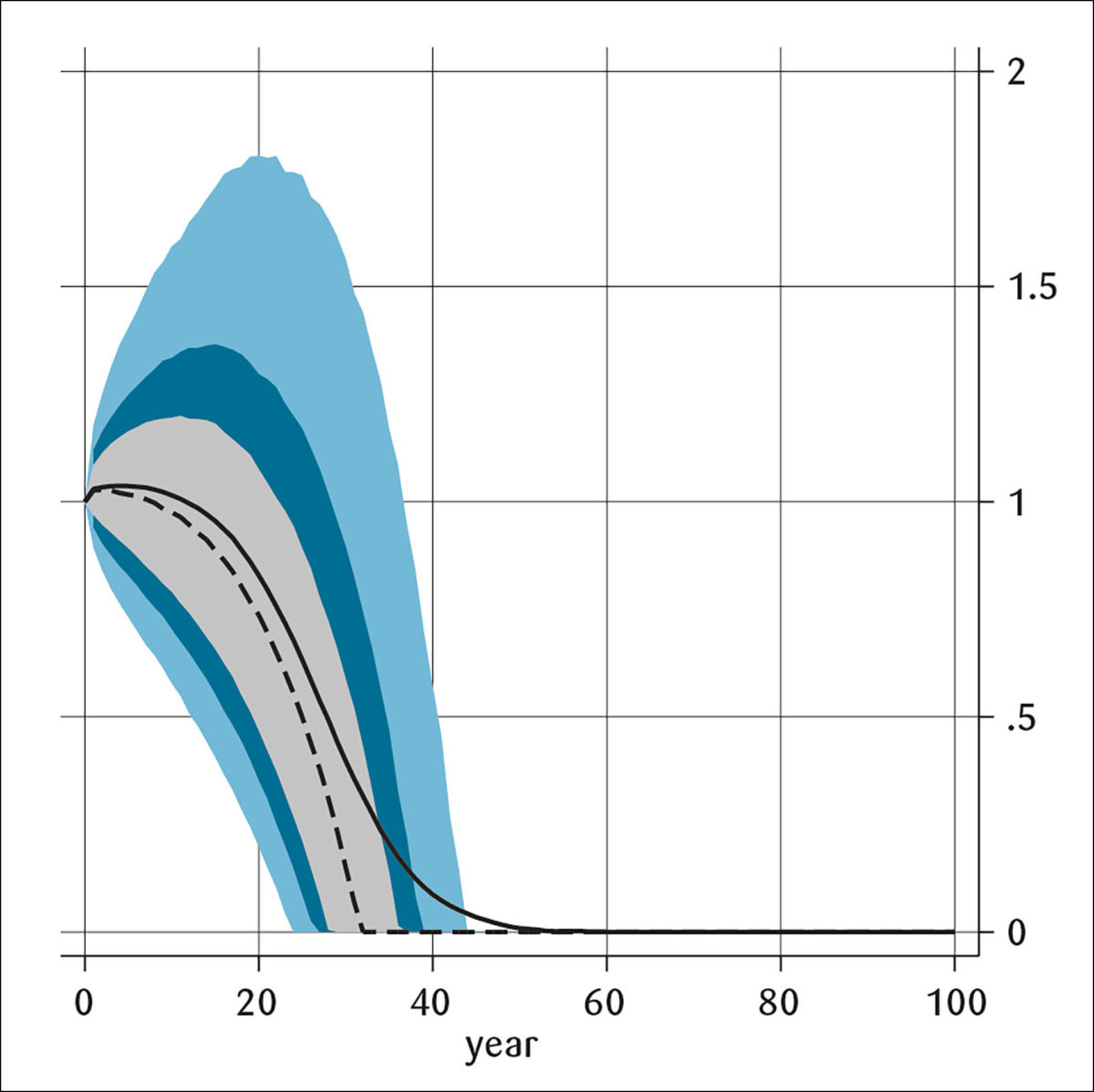
Simulering av verdien til oljefondet med en handlingsregel der man stabiliserer budsjettunderskuddet på 10% av BNP 100 år frem i tid. Heltrukken linje viser gjennomsnittet, stiplet linje viser median, grått bånd viser 50%, blått bånd viser 70% og lyseblått bånd viser 90% usikkerhetsintervall. Logaritmisk skala.
Figur 4 viser at hvis vi stabiliserer budsjettunderskuddet som andel av BNP omtrent på dagens nivå og det ikke kommer nye oljeinntekter, så er oljefondet brukt opp i løpet av en generasjon. Det skyldes at det ikke bare er 10 prosent av Fastlands BNP vi bruker hvert år, men også renters rente av dette beløpet. Dersom man stabiliserer budsjettunderskuddet på et lavere nivå vil oljefondet selvsagt vare lengre. Eksempelet viser tydelig at valg av finanspolitisk handlingsregel innebærer en avveining mellom stabil finanspolitikk og fordeling mellom generasjoner som jeg analyserer mer inngående i Wulfsberg (2022).
Motsyklisk finanspolitikk
Jeg har sett bort fra kostnader ved motsyklisk finanspolitikk ( ) som vi vet kan være betydelige. Disse kostnadene kan forsterke fallet i oljefondets verdi med dagens handlingsregel av samme grunn som beskrevet over. For å forstå hvorfor, anta at vi får en lavkonjunktur i år s. I dette året vil kostnadene ved motsyklisk politikk være positive og redusere verdien av oljefondet tilsvarende det året. Men i tillegg vil disse kostnadene redusere verdien av fondet i årene etter med rentes rente av ekstraavkastningen. Dersom i år s, mens i alle andre år får vi fra (4) at verdien til oljefondet blir
(6)
Dette innebærer både et skift nedover i medianbanen og resten av fordelingen i år s og en hurtigere tapping av oljefondet fordi rentes rente av fondet blir mindre. Motsatt vil et år med høykonjunktur gi negative kostnader ved motsyklisk politikk BtC+BtD<0 og øke verdien av oljefondet det året. I tillegg vil dette øke verdien av fondet i ettertid med rentes rente av ekstraavkastningen. Dette tilsvarer et skift oppover i medianbanen og resten av fordelingen. Selv om både konjunkturene og kostnadene ved motsyklisk politikk skulle være helt symmetriske vil variasjon i kostnadene ved motsyklisk finanspolitikk i seg selv forsterke fallet i verdien til oljefondet fordi variansen til fondets verdi øker. Dersom lavkonjunkturer er dypere og mer langvarige enn høykonjunkturer for eksempel som følge av et bindende gulv for pengepolitikken, eller dersom motsyklisk politikk er mer kostbar i lavkonjunkturer (i absoluttverdi), vil fallet i oljefondets verdi kunne bli ytterligere forsterket. Simuleringene som er gjengitt i Figur 1 kan derfor betraktes som et optimistisk anslag på verdiutviklingen til oljefondet.6
Handlingsregelen åpner som sagt også for å glatte budsjettunderskuddet ved brå og store endringer i oljefondets verdi. Dette trekker isolert sett i retning av mindre variasjon i finanspolitikken. På den andre siden kan økte budsjettunderskudd som følge av glatting føre til at det blir større variasjon i verdien av fondet noe Dybvig og Qin (2021) diskuterer. Glatting av budsjettunderskuddet kan altså føre til mer variasjon over tid og dermed en raskere tapping av oljefondets verdier.
Oppsummering
Analysen viser at handlingsregelen ikke sikrer verdien av oljefondet slik det påstås, snarere tvert imot. Simuleringene bygger ikke på strenge forutsetninger om optimaliserende adferd, kun på definisjonen av handlingsregelen (2), akkumuleringsidentiteten til oljefondet (1), samt forutsetningene om fremtidige oljeinntekter og konjunkturer som jeg har diskutert. Simuleringene er basert på en stokastisk fordeling av realavkastningen som bygger empiriske observasjoner av oljefondets verdi. Et optimistisk anslag er at medianverdien av oljefondet utgjør 64 prosent av initialverdien uten tilførsel av nye oljeinntekter.
Handlingsregelen har fungert godt i to tiår mens oljeinntektene har fylt opp fondet. En heldig utvikling i finansmarkedene har bidratt til ytterligere vekst. Dette har gitt rom for en gradvis økning i bruk av oljepenger i økonomien som nå er på et svært høyt nivå og er trolig med på å forklare den brede politiske støtten til handlingsregelen. Staten vil fortsatt ha betydelige oljeinntekter i flere år fremover som gir utsikter til enda høyere oljepengebruk. Men det er viktig å innse at handlingsregelen over tid ikke sikrer verdien av oljefondet og at den innebærer en svært uforutsigbar finanspolitikk. En ny finanspolitisk regel bør gi en mer forutsigbar finanspolitikk som i større grad er frikoplet fra variasjonen i internasjonale finansmarkeder. En mer stabil finanspolitikk vil nødvendigvis medføre mer ustabil verdi av oljefondet. Denne politiske avveiningen bør være sentral i valget av ny handlingsregel.
Referanser
Bjørnland, H. C. (2022). Vi må gjøre noe med oljepengebruken. Gjestekommentar i Dagens Næringsliv 10. februar.
Carpena, F. og F. Wulfsberg (2020). Scraping the GPFG Net Asset Value, Data Documentation. Upublisert notat, Oslomet.
Coiner, M. (1990). The Lognormality of University Endowment in the Far Future and its Implications. Economics of Education Review 9(2), 157–161.
Dybvig, P. H. og Z. Qin (2021). How to Squander Your Endowment: Pitfalls and Remedies. Upublisert notat. http://dx.doi.org/10.2139/ssrn.3939984
Henriksen, E. (2022). Planen var så god at finansiell risiko har tatt plassen til oljeprisrisiko. Samfunnsøkonomen 136 (4), s. 33–41.
Ho, G. P., H. A. Mozes og P. Greenfield (2010). The Sustainability of Endowment Spending Levels: A Wake-up Call for University Endowments. Journal of Portfolio Management 37(1), 133–146.
Holden, S. (2022). Justering av handlingsregelen – uttak fra Oljefondet basert på kontantstrømmer? Samfunnsøkonomen 136 (4), s. 70–81.
Kjelsrud, A. (2017). Handlingsregelen og endringer i Statens pensjonsfond utland. SSB Økonomiske analyser
Meld. St. 29 (2000–2001). Retningslinjer for den økonomiske politikken.
Meld. St. 1 (2021–2022). Nasjonalbudsjettet 2023.
Mork, K. A., H. A. Trønnes og V. S. Bjerketvedt (2022). Capital Preservation and Current Spending with Sovereign Wealth Funds and Endowments Funds: A Simulation Study. Upublisert notat.
NOU (2016). Aksjeandelen i Statens pensjonsfond utland. Norges offentlige utredninger 2016:20.
Rådgivende utvalg for finanspolitiske analyser (2022a). Bakgrunnstekst 4: Sårbarhet ved Oljefondets rolle. https://www.regjeringen.no/no/tema/okonomi-og-budsjett/norsk_okonomi/finansdepartementets-radgivende-utvalg-f/id654149/
Rådgivende utvalg for finanspolitiske analyser (2022b). Uttalelse. https://www.regjeringen.no/no/tema/okonomi-og-budsjett/norsk_okonomi/finansdepartementets-radgivende-utvalg-f/id654149/
Wulfsberg, F. (2018). Har vi klart å spare oljeinntektene? Samfunnsøkonomen 132 (3), 33–38.
Wulfsberg, F. (2022). Fiscal policy rules and the trade-off between sovereign wealth and economic stability. Upublisert notat, Oslomet.
Wyplosz, C. (2019). Fiscal Discipline: From Theory to Practice. https://www.charleswyplosz.info/_files/ugd/60d1ea_ebc6db9e9ffa4023-a9467634d31e0f52.pdf
Aase, K. K. og P. Bjerksund (2021). The Optimal Spending Rate Versus the Expected Real Return of a Sovereign Wealth Fund. Discussion Papers 2021/1, Norges Handelshøyskole.
Fotnoter:
- Takk for gode kommentarer fra en anonym konsulent, Lars-Erik Borge, Steinar Holden, Gisle James Natvik og seminardeltakere ved NTNU og Oslomet. ↩︎
- https://k7bulletin.no/nicolai-tangen-om-nhh-dere-gar-i-helt-feil-retning/ ↩︎
- Senere Ho mfl. (2010) og også nylig poengtert av Dybvig og Qin (2021), Aase og Bjerksund (2021) og Mork mfl (2022). ↩︎
- Handlingsregelen er beskrevet i Meld. St. 1 (2021–2022), boks 3.2, side 72–73. ↩︎
- Tilsvarende viser Figur 2 variasjonen i finanspolitikken hvis vi baserte bruken av oljepenger på 2,5 prosent av oljefondet i stedet for 3 prosent. ↩︎
- Mork mfl. (2022) finner at glatting og motsyklisk konjunkturpolitikk (automatiske stabilisatorer og diskresjonære tiltak) øker tappingen av medianverdien av oljefondet med 200–400 milliarder NOK i løpet av 40 år (Tabell 3). ↩︎
