Formueskatt med redusert skattegrunnlag for aksjer
Vi viser at et redusert skattegrunnlag for aksjer, i tillegg til å vri investeringer fra rentepapir til aksjer, også vrir verdsetting av aksjer, mer spesifikt at det øker verdien av lite risikable aksjer, og senker verdien for risikable aksjer. Denne vridningen er uheldig om en ønsker at nordmenn investerer i mer risikable prosjekt for å få fortgang i omstillingen bort fra en i stor grad petroleumsbasert økonomi.
Formueskatt med redusert skattegrunnlag for aksjer1
Innledning
For et gitt beløp til finansinvesteringer er en lik formueskatt på alle formuesobjekt nøytral, dvs. endrer ikke verdien av aksjer/prosjekt. Dette er et kjent resultat, men trolig først publisert i Bjerksund og Schjeldrup (2021). NOU 1991: 17 beskriver t.d. nøytralitet som at atferden ikke endres, men ser ikke direkte på verdsetting.
I Norge er formueskattesatsen essensielt lik for alle skatteobjekter. Men skattegrunnlaga, dvs. den skattemessige verdien relativt til den reelle verdien, varierer mye, fra 25 prosent på primærboliger til 100 prosent på rentepapirer, se Skatteetaten (2021). Dermed varierer den effektive formueskattesatsen og nøytraliteten oppheves. Her tar vi bare opp forholdet mellom aksjer og (sikre) rentepapir.
De siste åra er skattegrunnlaget for formueskatten på aksjer nesten halvert i forhold til rentepapir. Dette har opplagt økt verdien av å investere i aksjer i forhold til rentepapir. Vi viser at det reduserte skattegrunnlaget også vrir verdsetting av aksjer, mer spesifikt at det øker verdien av lite risikable aksjer, og senker verdien for risikable aksjer for norske investorer. Forskjellen i verdsetting er liten på kort sikt, men øker ekspotensielt med tidshorisonten.
Vi tar hensyn til usikkerhet vha. kapitalverdimodellen, som vi først skisserer. Vi ser så på virkningen av en formueskatt med redusert skattegrunnlag for børsnoterte aksjer i en periode. Deretter ser vi på unoterte aksjer, før vi utvider til flere perioder. Til slutt diskuterer vi kort resultata.
Kapitalverdimodellen
Gitt n usikre aksjer, hvor aksje j har pris i dag og (usikker) framtidig pris og ett sikkert verdipapir med (total-) avkasting R. La markedsporteføljen, , dvs. porteføljen av alle markedsomsatte aksjer, hvor er antall verdipapir av type j. Kall den normaliserte markedsportefølje, med pris 1 i dag.
La S være de mulige framtidige tilstandene og la være sannsynligheten for tilstand , og la forventningsverdien til den stokastiske variablen . La være kovariansen mellom framtidsverdiene til i og j og betaen til framtidsverdien til prosjekt j (relativt til den normaliserte markedsporteføljen). Betaen uttrykker risikoen til verdipapir j, relativt til risikoen til den normaliserte markedsporteføljen.
Kapitalverdimodellen for verdier sier at risikopremien (dvs. den forventa merverdien i forhold til en tilsvarende sikker investering) til ethvert markedsomsatt verdipapir j er proporsjonal med betaen til verdipapiret, med risikopremien til markedsporteføljen som proporsjonalitetsfaktor, dvs.
(1)
Løser vi denne med hensyn på prisen av aksjen i dag, pj0, får vi kapitalverdien på verdsettingsform, dvs. at for alle markedsomsatte aksjer j gjelder at:2
(2)
Nåverdien av framtidsverdien til aksje j er altså sikkerhetsekvivalenten til framtidsverdien, , diskontert med den sikre avkastinga. Ved fravær av arbitrasje, som innebærer at like framtidige kontantstrømmer må ha samme verdi i dag, gjelder (2) også for alle investeringsprosjekt.
Formueskatt
La alle størrelsene ovafor være før formueskatt. Gitt en størrelse, x, før utbytteskatt, la , være den samme størrelsen med formueskattesats og skattegrunnlag for aksjer, g, som andel av verdien. Sikre investeringer skattlegges fullt ut.
Etter formueskatt blir da framtidsverdien av å investere i en aksje j, , hvor , den forventa framtidsverdien , og den sikre avkastinga , hvor . La (den direkte) skattefordelen for aksjer, være forholdet mellom det en har igjen av ei krone etter formueskatt ved aksjer i forhold til rentepapirer. Vi antar , så skattefordelen . Skattefordelen med aksjer øker med skattesatsen og reduseres med skattegrunnlaget.
I Norge er (unntatt i Bø kommune) og , så , , og , se Skatteetaten (2021).
Markedsporteføljen endres bare ved nyemisjoner o.l.. I tillegg antar vi en liten åpen økonomi, i betydningen at verdipapirprisene og R er gitt. Dermed endres heller ikke den normaliserte markedsporteføljen av formueskatten, dvs. .
I det følgende antar vi at aksje j har verdi før formueskatt . Da er framtidsverdien av aksjen lik avkastinga på denne, og vi lar være den vanlige betaen til avkastinga.
En periode
For en markedsomsatt aksje j er videre betaen etter skatt lik den før, ved definisjonene og lineariteten av kovariansen i begge argument,
Nåverdien av framtidsverdien til en markedsomsatt aksje j etter skatt blir da ved kapitalverdimodellen på verdsettingsform,
(3)
Ved kapitalverdimodellen før formueskatt, (2), siden blir nåverdien av framtidsverdien
(4)
Uten noen skattefordel for aksjer, dvs. om , blir verdien av aksjen for en norsk investor uendra med formueskatt, dvs. . Dette er nøytralitetsresultatet vi nevnte i innledninga. Intuisjonen er at formueskatten reduserer avkastinga med samme faktor, som avkastinga, som gir uforandra nåverdi.
Med en skatterabatt på aksjer, dvs. har en økt formueskatt en positiv virkning på aksjeverdien, , for lite risikable aksjer, dvs. om og negativ virkning for mer risikable aksjer, dvs. om . Altså øker aksjeverdiene for foretak med lav markedsrisiko (målt ved beta) med formueskatt, mens de reduseres med høy. En forklaring er at aksjer med lav risiko er nære substitutt til sikre verdipapir, som er hardere skattlagt. I neste avsnitt gir vi en litt annen forklaring.
Litt overraskende avhenger verdien etter skatt i (3) bare av betaen til aksjen, og skattefordelen for aksjer, . Verdien av å investere ei krone i aksje j avhenger altså verken av forventa avkasting eller den sikre avkastinga. Dette er en konsekvens av det underliggende nøytralitetsresultatet for
Formueskatt med lavere skattegrunnlag for aksjer fører altså til nordmenn får en høyere verdsetting av lite risikable markedsomsatte aksjer og en lavere for slike med høy risiko. Verdsettinga endres derimot ikke for utenlandske investorer, som ikke er skattlagt. Med økt formueskatt og skatterabatt for aksjer øker dermed nordmenns relative andel i markedsomsatte lavrisikoaksjer, mens den avtar for høyrisikoaksjer. Denne vridningen er uheldig om en ønsker at nordmenn investerer i mer risikable prosjekt for å få fortgang i omstillingen bort fra en i stor grad petroleumsbasert økonomi.
Fra eiersida blir det ofte hevda at formueskatten favoriserer utenlandske investorer. Resultatet ovafor viser at dette feil uten en verdsettingsrabatt for aksjer. Men verdsettingsrabatten gjør at det er noe i dette for aksjer med høy risiko, sjøl om det er motsatt for aksjer med lav risiko.
Alternativavkastingsformulering
Vi kan vise essensielt samme resultat ved hjelp av den mer vanlige alternativavkastingsformuleringa av kapitalverdimodellen. Siden , blir fra (1) alternativavkastinga til en aksje j etter formueskatt . Setter vi inn og dividerer på , blir alternativavkastinga til det framtidige forventa kontantoverskuddet til en aksje/prosjekt før formueskatt,
(5)
Altså virker formueskatten med en skatterabatt for aksjer på samme måte som en reduksjon av alternativavkastinga med faktoren , den reduserer alternativavkastinga for og øker den for . Dermed blir relativt sikre aksjer/prosjekt mer lønnsomme for en norsk investor og mer usikre aksjer/prosjekt mindre lønnsomme med formueskatt enn uten, illustrert i figuren nedafor, hvor den heltrukne linja er alternativavkastinga uten formueskatt og den stipla med.
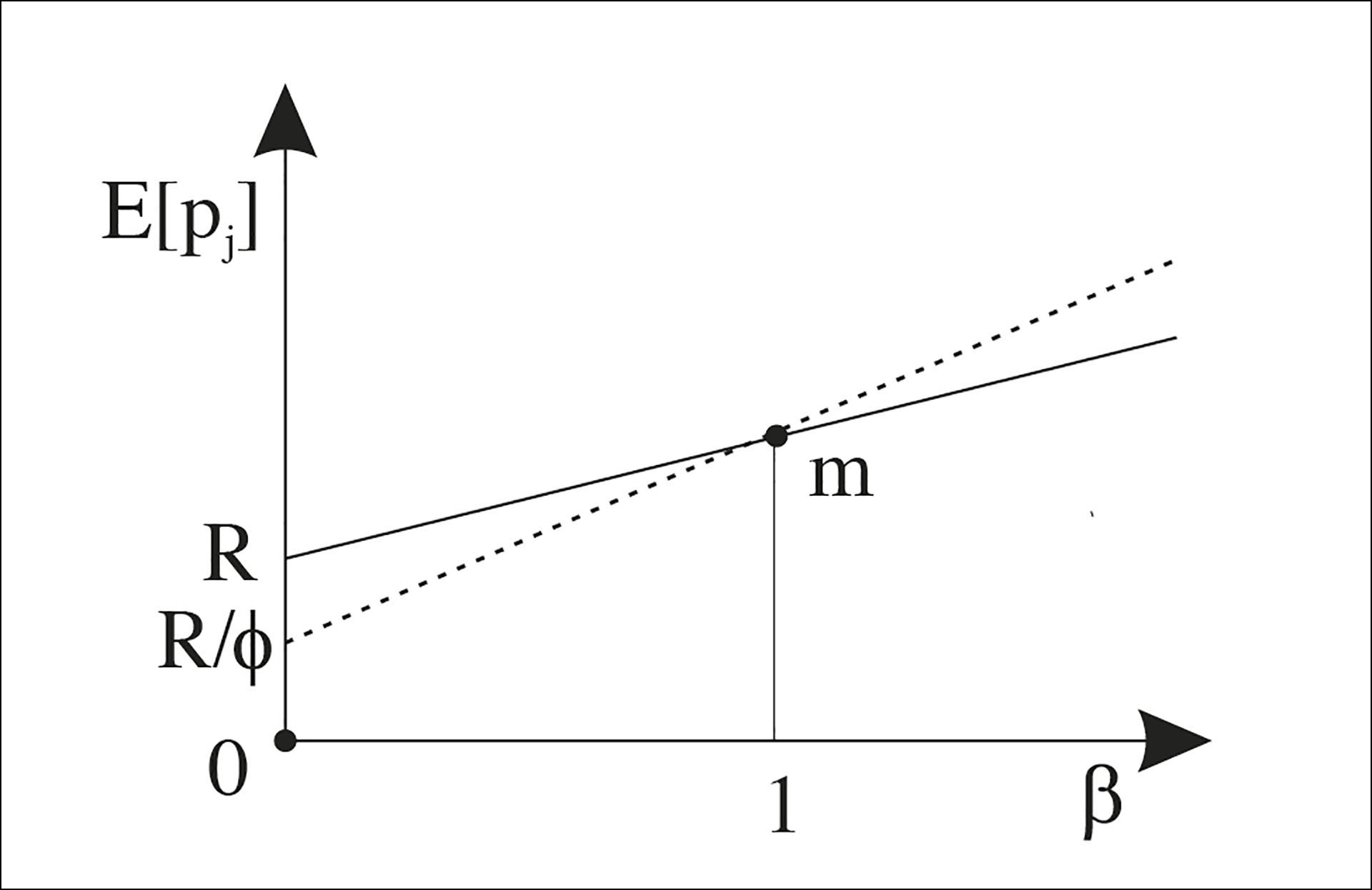
Figur 1
Denne formuleringa er litt enklere for en periode enn nåverdiformuleringa ovafor, men nåverdiformuleringa er lettere å utvide til flere perioder. Det er også lettere å tenke på verdiendringa direkte enn på endringa i alternativkostnad.
Unoterte foretak
Vi har så langt bare sett på markedsomsatte aksjer. Unoterte aksjer verdsettes skattemessig til bokført verdi, som vanligvis er adskillig lavere enn markedsverdien. La være forholdet mellom bokført verdi og markedsverdi for en unotert aksje j.3 Da blir andelen av formuen etter skatt for j, . La skattefordelen til j (relativt til en notert aksje), . Går vi fram som ovafor, får vi for en slik unotert aksje j at betaen blir og nåverdien av framtidsverdien etter skatt,
Altså er forholdet mellom nåverdiene av framtidsverdiene etter formueskatt av et foretak om det er unotert og notert lik den direkte skattefordelen til det unoterte foretaket. I det typiske tilfellet med , fører dette til mer investeringer i unoterte foretak enn uten formueskatt. Skattefordelen til unoterte foretak forsterkes trolig av at humankapital ikke blir regna som bokført kapital, og at unoterte foretak dermed substituerer seg mer i retning av slik kapital. Det siste er forklaringa Bjørneby mfl. (2020) gir for sitt overraskende resultat om at høyere formueskatt øker sysselsettinga.
Vi får nå at om
altså vil, ikke overraskende, litt mer risikable aksjer bli mer lønnsomme med formueskatt om de er unoterte enn om de er børsnoterte. For , blir , så skattefordelen til den unoterte aksjen, Da øker grenseverdien ovafor fra til .
Flere perioder
Vi ser igjen på en markedsomsatt aksje, j, og bruker indeks t for tidspunkt t. Anta at den sikre avkastinga og den normaliserte markedsporteføljen er konstant over tid, dvs. , og at framtidsverdiene av ei krone for verdipapiret er ukorrelerte, dvs, om .
La som før være nåverdien av framtidsverdien etter en periode av ei krone investert. Nåverdien av framtidsverdien av ei krone investert i verdipapir j på tidspunkt 0, med tidshorisont T blir nå etter skatt
Hvorfor blir det slik? Ei investering på ei krone på tidspunkt null gir fra (3) og (4) en framtidsverdi med sikkerhetsekvivalent på tidspunkt 1, på tidspunkt 1. Reinvestert gir denne en sikkerhetsekvivalent på tidspunkt 2. Diskonterer en dette tilbake til tidspunkt 0 med får vi , osv.
Eksempel
For Norge er den heltrukne linja verdien med en ettårig tidshorisont
, og den stipla linja den for en tiårig horisont,
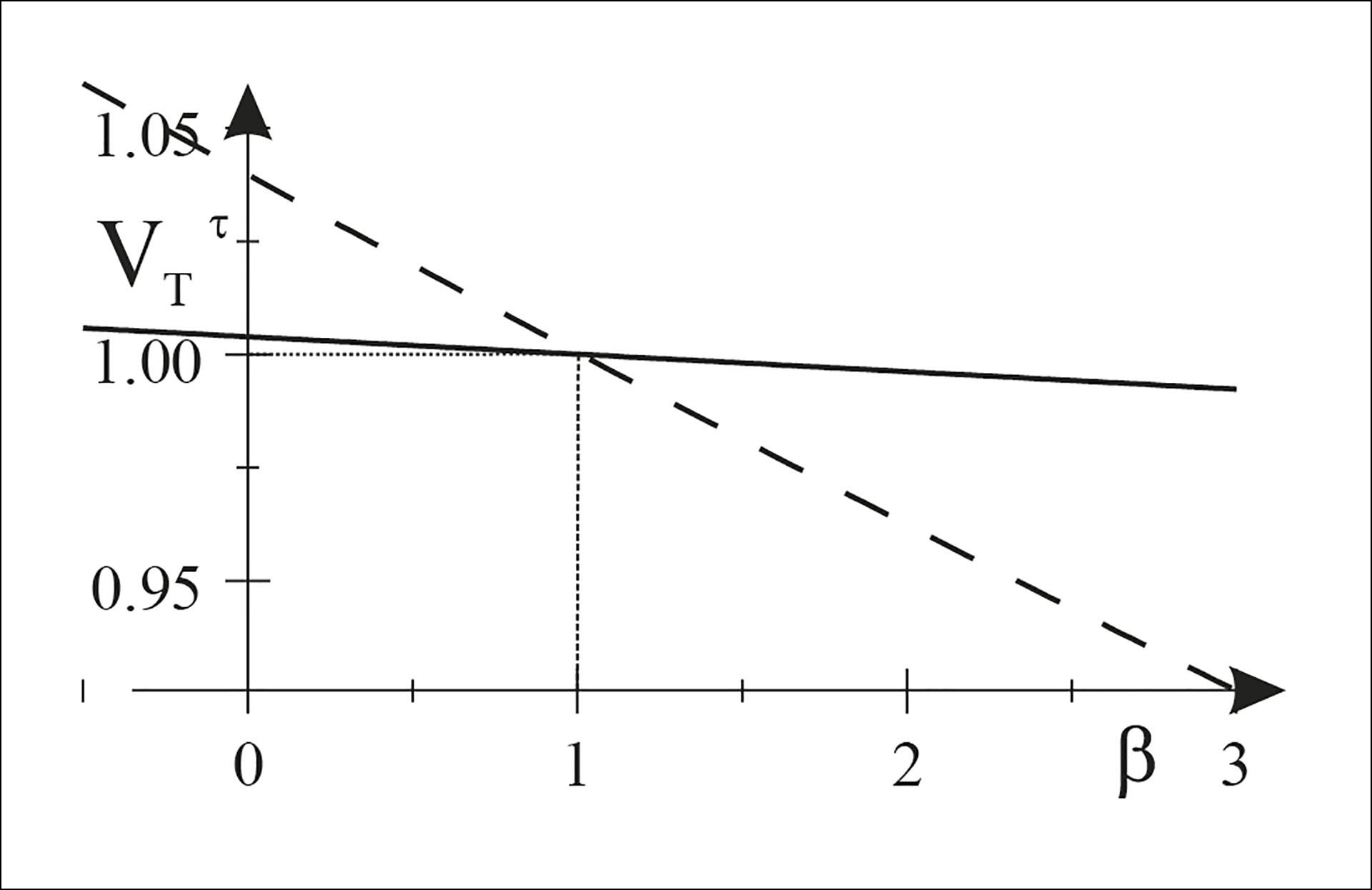
Figur 2
Diskusjon
Kapitalverdimodellen ovafor tar formuen til investeringsformål for gitt. Ved å endogenisere sparinga, reduseres som vanlig sparinga til fordel for konsum av formueskatten. Dermed påvirker sjøl en uniform formueskatt investeringer. Men siden de skikkelig rike eier en stor del av aksjene, og en kan regne med at disse har marginal konsumtilbøyelighet null, er denne effekten relativt liten totalt sett. Effekten kan dermed reduseres med et solid bunnfradrag i formueskatten.
Vi har antatt at en ikke kan unngå formueskatten. Men det er mulig ved å flytte utenlands, rett nok til en relativt høy kostnad for mange. Dermed kan en ikke ha særlig høy formueskatt i et enkelt land, i alle fall uten formueskatt på utflytting/endring av statsborgerskap.
Formueskatten reduserer sjølsagt formuen til en investor, som indirekte kan påvirke norske investorers andel av det norske markedet. Dette gjelder imidlertid alle skatter som investorer betaler, og er ikke spesielt for formueskatten.
Vi har her bare sett på verdsetting i samband med formueskatt. NOU 1991: 17 og mer nylig Scheuer og Slemrod (2020) har interessante diskusjoner av formueskatt i et videre perspektiv.
Referanser
Bjerksund, P. og G. Schjeldrup (2021). Investor asset valuation under a wealth tax and a capital income tax. International Tax and Public Finance. https://link.springer.com/article/10.1007/s10797-021-09691-0
Bjørneby, M., S. Markussen og K. Røed (2020). Does the Wealth Tax Kill Jobs? IZA Discussion paper no. 13766. http://hdl.handle.net/10419/227293
Copeland, T. E., J. F. Weston og K. Shastri (2014). Financial Theory and Corporate Policy. Pearson.
NOU 1991: 17. Bedrifts- og kapitalbeskatningen. Beskatning av formue. https://www.nb.no/items/URN:NBN:no-nb_digibok_2007112800051
Sandvik, B. (2016). Formueskatt på unoterte foretak. Samfunnsøkonomene 130 (3), 5–8.
Scheuer, F. og J. Slemrod (2020). Taxing Our Wealth. CEPR Discussion Papers 15481.
Skatteetaten (2021). Satser for: Formuesskatt og verdsettingsrabatter. https://www.skatteetaten.no/satser/formuesskatt/
Fotnoter:
- Eirik.Hansen@student.uib.no og Bjorn.Sandvik@uib.no. Artikkelen bygger på Eiriks bacheloroppgave i samfunnsøkonomi våren 2021. Takk til en anonym referee for flere gode forslag til forbedringer. ↩︎
- Kapitalverdimodellen på denne formen finner en i Copeland m. fl. (2014, ligning (20)). ↩︎
- Her antar vi at forholdet mellom bokført verdi og framtidig markedsverdi er gitt. Med bare en periode er det mer realistisk å se på den bokførte verdien som gitt, uten at det endrer resultata nevneverdig, se Sandvik (2016) for dette tilfellet, rett nok uten verdsettingsrabatt. ↩︎

