Dynamisk modellering og framskrivning av nye smittede og innlagte med Covid-19 i Norge
I denne analysen presenteres det modellbaserte prognoser for daglige antall nye smittede og for antallet personer som er innlagte på sykehus med påvist Covid-19. Modellen, CovidMod, er komplementær til framskrivningsmetodene som FHI har benyttet til å lage prognoser på nasjonalt nivå under pandemien. Framskrivningene med CovidMod i 2021 har resultert i en database med daglige prognoser og prognosefeil. En sammenligning med FHIs tre ukers prognoser viser at CovidMod har hatt lavere RMSFE («Root Mean Squared Forecast Error») for både nye smittetilfeller og for antallet pasienter som er innlagt på sykehus. Den store smittebølgen i november og desember 2021 utgjør en interessant «case». I modellen forklares denne bølgen av Deltavarianten av viruset, og av gjenåpningen av samfunnet som hadde funnet sted tidligere på høsten. Til sammen bidro disse faktorene til at modellens kritiske parameter ble større enn +1, som ga en eksplosiv utvikling i prognosene. I modellen skjedde dette på tross av at det er estimert signifikante effekter av vaksinasjonsgraden.
Dynamisk modellering og framskrivning av nye smittede og innlagte med Covid-19 i Norge1
Innledning
Under pandemien har det vært stor interesse for data og prognoser om hvordan Covid-19 sprer seg i Norge. Sammenhengen mellom nye smittede og antallet pasienter som blir innlagt på sykehus med Covid-19 inngår i vurderingen av den belastningen som helsevesenet står overfor under pandemien. Data og prognoser for nye smittede og antallet pasienter blir dermed også viktige for de politiske prosessene som tar sikte på å begrense alvorlig sykdom, og for å bevare et godt helsetjenestetilbud under pandemien.
En term som allmenheten har blitt godt kjent med er reproduksjonstallet, R. Begrepsmessig viser R hvor mange personer én person med koronasmitte smitter videre. Hvis R=1 vil hver smittede person smitte én annen person. Et høyere R-tall kan varsle en kraftigere spredning av viruset, som på noe sikt kan overvelde helsevesenet. Om tallet ligger under +1, er det derimot mindre smittespredning, og man kan si at man har viss kontroll over utviklingen. I Norge er estimering og kalibrering av R en integrert del av FHIs modellering og simulering av pandemien. Reproduksjonstallet er en nøkkelparameter i den prognosemodellen som FHI bruker i sine framskrivninger med tre ukers horisont.2
FHIs prognoser er basert på epidemiologisk ekspertise i kombinasjon med presis matematisk modellering. Matematisk presisjon er imidlertid ikke en tilstrekkelig betingelse for treffsikre framskrivninger, noe som er velkjent fra evaluering av makroøkonomiske prognoser. Forklaring på store prognosefeil er som regel at det skjedde et regimeskifte i økonomien under prognoseperioden, på en måte som ikke var blitt innarbeidet i modellen på opprinnelsesdatoen til prognosen. Dermed kan vi ofte observere at prognosene blir upresise, og at de noen ganger sporer helt av, fordi prognosen styrer mot en likevekt som ikke lenger finnes i data etter at regimeskiftet har inntruffet.
Selv om alle modellbaserte prognoser er sårbare overfor strukturelle brudd kan det være forskjeller i graden av utsatthet. Det samme kan sies om hvor adaptive de forskjellige framskrivningsmetodene er overfor et regimeskifte som har inntruffet før opprinnelsesdatoen til prognosen, Nymoen (2019, kap. 12). Tilnærminger som er komplementære til epidemiologiske strukturmodeller omfatter logistiske vekstkurver, dynamiske trendmodeller, autoregressive modeller og robuste prognosemetoder, jf. Harvey og Kattuman (2021), Castle mfl. (2020) blant andre.
I denne artikkelen presenteres resultater fra et prosjekt der idéen har vært at nye smittede og antallet Covid-19 pasienter utgjør et dynamisk system. Med andre ord, en tilnærming som ikke er så forskjellig fra det vi kjenner fra makroøkonometrisk modellering. Modelleringsopplegget tilhører kategorien autoregressive modeller. Med et slik utgangspunkt blir ikke R-tallet en tidsuavhengig parameter. R-tallet er i stedet en tidsavhengig variabel i en modell som allerede framskriver nettopp antallet nye smittede og innlagte på sykehus med Covid-19.
I modellen er det andre parametere enn R-tallet som styrer prognosene på tre ukers sikt. Spesielt viktig er den lavfrekvente roten i den karakteristiske ligningen som er tilordnet prosessen for antallet nye tilfeller. Denne kritiske parameteren kan estimeres fra tidsrekkedataene. Stabiliteten (over tid) i den kritiske parameteren kan undersøkes på daglig basis. Graden av invarians i parameteren kan testes. Indikatorer for ikke-farmasøytiske tiltak som kan påvirke den kritiske parameteren kan bli innarbeidet i modellen. Det samme gjelder effekter av nye virusvarianter og av vaksinasjonsgraden i befolkningen. Artikkelen inneholder sammenligninger mellom modellprognoser og prognoser fra FHI. Prognosene for november og desember 2021 sammenlignes grafisk. For den lengre perioden, fra mars til november 2021 skjer sammenligningen ved hjelp av standardmålet RMSFE («Root Mean Squared Forecast Error»).
Modellbeskrivelse
Framskrivninger som var basert på autoregressiv modellering av nye smittede og innlagte ble publisert på nettstedet Normetrics under den første bølgen, vinteren 2020. I mai 2020 var imidlertid tallene for nye smittede og sykehusinnleggelser blitt så lave at det ikke var noe poeng å fortsette med framskrivningene, før et eventuelt nytt utbrudd.3 I mars 2021 befant vi oss imidlertid i en tredje bølge, med smittetall som var langt høyere enn under den første bølgen, og med stigende antall sykehusinnleggelser. Det var derfor interessant å ta fram modellen fra første bølge, og re-spesifisere de empiriske relasjonene på de lengre tidsseriene. Med oppstart 17. mars 2021 har opplegget, som vi heretter referer til som CovidMod, blitt brukt til å lage prognoser hver virkedag. Horisonten for prognosene har hele tiden vært 21 dager.
Det er fire endogene variable i modellen:
- NSt, nye smittede med Covid-19, dag t.
- SSt, akkumulert antall nye smittede, dag t.
- NINLt, nye innlagte med Covid-19, dag t.
- INLt, antall innlagte med Covid-19, dag t.
Alle variable har antall personer som enhet, og gjelder landet som helhet. Datakilden for NSt er FHI, «Meldingssystem for smittsomme sykdommer» (MSIS).4 Tallene er ordnet etter datoen på avlagt test. Dette betyr at det vil være noe avvik mellom disse tallene og tallene i VG, som er antallet nye smittede etter registreringsdato. Det er enda tydeligere sesongmønster i tidsserien NSt enn i VGs tall (lavest tall i helgene). Men trendene i de to seriene er like, de er bare litt forskjellige målinger av samme fenomen.
Kilden for antall innlagte, INLt, er Helsedirektoratets statistikk over antall innlagte med påvist Covid-19.5 Data for nye innlagte er lastet ned fra FHIs internettsider.6
Sammenhengen mellom nye smittede og akkumulert antall smittede ivaretas av definisjonsligningen:
(1)
Det er også en enkel «law of motion» for antall innlagte:
(2)
der depresieringsraten er estimert til 0,1 ved bruk av vanlig MKM og en forholdsvis kort estimeringsperiode.
Med (1) og (2) på plass, er det bare NStog NINLt som trenger å bli modellert økonometrisk. I resten av dette avsnittet ser vi nærmere på modelligningene for disse to variablene.
Fra begynnelsen av prosjektet ble det benyttet lineære funksjonsformer. Andre tilnærmingsmåter, som kunne omfatte logistiske vekstkurver, dynamiske trendmodeller eller såkalt robuste prognosemetoder, kan være av interesse og ha stor potensiell nytteverdi, jf. Castle mfl. (2021) og referansene der.
På forenklet form er modelligningen for NSt:
NSt
= {0,073 + 0,019 ALPHAt − 0,013 MIDMAR21t
+ 0,014 DELTAt + 0,016 OPENUPOCT21t
− 0,041 VAKSt} (SSt−1 − SSt−14) (3)
Koeffisientene i (3) blir re-estimert på hver prognosedato, etter at datasettet er blitt oppdatert. Estimeringsperioden som ble benyttet til (3) var fra 22. februar 2021 til 20. november 2021. Estimeringsmetoden var vanlig MKM. I den operasjonelle modellen inngår det også «lagget» egendynamikk, og impulsdummier. Detaljerte estimeringsresulatene er tilgjengelig på Normetrics.no.
For å tolke modelligningen ser vi på leddet som står rett til høyre for likhetstegnet, og kommenterer deretter de øvrige leddene i (3). Antall nye smittede vil avhenge av den smitten som allerede er i befolkningen, som imidlertid er en uobserverbar variabel. I ligning (3) er (SSt−1 – SSt−14) brukt i rollen som indikator for smitten i befolkningen.
På grunn av definisjonsligningen (1) er imidlertid (SSt−1 – SSt−14) identisk med summen av nye smittede over 14 dager:
(4)
Modelligning (3) er derfor en autoregressiv modell. Dermed kan vi multiplisere den første koeffisienten i (3) med 13 og tolke produktet som et estimat på den karakteristiske roten tilordnet den lavfrekvente delen av NS-prosessen, Bårdsen og Nymoen (2014, kapittel 7.4). Dette blir en kritisk parameter i modellen, som vi kan kalle k, og som det vil være interessant å følge med på. Isolert sett innebærer k > 1 at modellprognosen vil være preget av eksponentiell vekst, Vi ser at k er estimert til 0,95 i (3), som imidlertid er betinget på faktorer som fanger opp at den kritiske parameteren har variert i løpet av pandemien på grunn av ikke-farmasøytiske tiltak, virusmutanter og økende vaksinasjonsgrad i befolkningen. Disse faktorene er representert ved de multiplikative leddene i (3). De nye variablene som inngår i de leddene er:
- MIDMAR21, en trinn-dummy for ikke-farmasøytiske tiltak vinteren 2021.
- OPENUPOCT21, en trinn-dummy for gjenåpningen høsten 2021.
- ALPHA og DELTA er trinn-dummier for «UK» virusvariant og for Deltavarianten.
- VAKS representerer vaksinasjonsgraden i den voksne befolkningen. Den stiger monotont med start 16.12.2020.7
Ifølge modellen økte k da den såkalte engelske varianten (representert ved ALPHA) kom til landet. De ikke-farmasøytiske tiltakene vinteren 2021 (MIDMAR21) virket i motsatt retning. Trinn-dummien for Delta-varianten bidrar derimot i retning av eksponentiell vekst. Det samme gjelder dummien for den nasjonale gjenåpningen høsten 2021.
Det kan nevnes at koeffisienten til dummiene er åpen for ytterligere tolkning. For eksempel er DELTA-dummyen satt til 1 fra midten av juli 2021. Da var samfunnet allerede åpnere enn tidligere under pandemien, og den estimerte koeffisienten kan i noen grad reflektere økt smitte på grunn av økte reiseaktivitet og et mer vanlig sosialt liv.
Alt i alt, med de verdiene som høyresidevariablene i (3) hadde ved slutten av estimeringsperioden, var implikasjonen at k > 1 ved slutten av november. Konkret, med vaksineindikator lik 0,75, blir anslaget k = 1,07. Dermed predikerte ligningen høyere tall for NS utover i desember, slik det blir vist i avsnittet om framskrivninger under smittebølgen i november og desember 2021.
Den andre modellerte relasjonen bestemmer nyinnleggelser på dag t. På forenklet form, og med samme sluttdato for estimeringsperioden som for NSti (3):
(5)
I følge denne modelligningen vil høyere smitte i befolkningen, gjennom økt (SSt−3 − SSt−19) etterhvert føre til at flere personer vil bli lagt inn på sykehus med påvist Covid-19. Imidlertid påvirkes denne viktig sammenhengen av endringer i viruset (det er estimert en effekt av Alphavarianten), vaksinasjon og ikke-farmasøytiske tiltak.8
Med unntak av identiteten (1) er det tilfeldige restledd i ligningene i CovidMod. De datagenererende prosessene til nye smittede og innlagte er ukjente og komplekse, mens forklaringsmodellene er relativt enkle. Det er derfor mange faktorer som inngår i restleddene. Ikke minst har importert smitte vært viktig under pandemien. Denne driveren får vi imidlertid hverken tatt hensyn til, eller får kontrollert for i CovidMod.
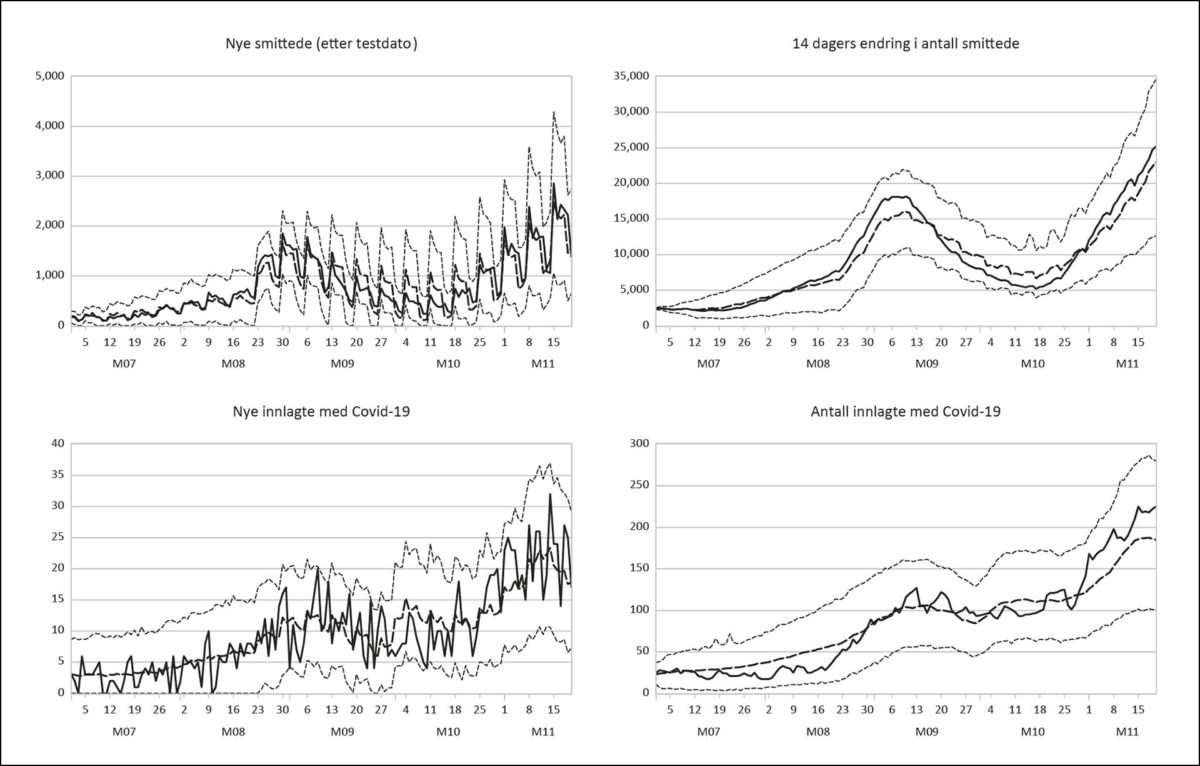
Restleddene bidrar til at det vil være betydelig spredning av observasjoner over og under banene som viser simulerte verdier for INL (nye smittede), SS (akkumulert antall smittede), NINL (nyinnleggelser) og INL (innlagte). Dette er illustrert i Figur 1 som viser hvordan modellen simulerte utviklingen fra 1.7.2021 til 20.11.2021.
Simuleringene er basert på faktiske tall for vaksineindikatoren VAKS, og betinger også på trinn-dummiene for mutasjoner og på ikke-farmasøytiske tiltak.
I praktisk prognosearbeid vil vi ikke kunne betinge på nye mutasjoner som inntreffer i prognoseperioden, etter opprinnelsesdatoene for prognosene. Utviklingen i vaksinasjonsgraden vil også være usikker på prognosetidspunktet. Figur 1 antyder derfor en bedre treffsikkerhet enn det man kan regne med i praktisk prognosearbeid med denne modellen. I et eget avsnitt ser vi nærmere på hvordan prognosene som ble laget i sanntid traff utviklingen under den store bølgen i november og desember 2021. I et annet avsnitt presenteres det resultater for et standardmål for prognosenøyaktighet over en lengre periode, fra mars til desember i 2021.
Tidsvarierende R-tall
I Norge beregnes reproduksjonstallet R av FHI som en integrert del av deres epidemiologiske modellering. Reproduksjonstallet er også en nøkkelparameter i modellen som brukes til FHIs prognoser med 21 dagers horisont. Dette omtaler FHI som beskrivelser av sykdomsbildet de nærmeste tre ukene fram i tid dersom den nåværende utviklingen fortsetter uendret. FHI kalibrerer modellen og estimerer reproduksjonstallet slik at modellen tilpasses sykehusinnleggelser og testdata både på nasjonalt nivå og på fylkesnivå.
Imidlertid er ikke den norske metoden for å tallfeste R-tallet helt representativt for det som gjøres i andre land. I for eksempel Tyskland er det nasjonale R-tallet gjennomsnittet av nye tilfeller de siste fire dager, delt på gjennomsnittet de foregående fire dagene, jf. Harvey og Kattuman (2021).
Mer generelt:
(6)
hvor summen i nevneren begynner på lag r og summene i teller og nevner kan overlappe hverandre. Etter litt algebra kan Rt,r,pskrives som:
(7)
der ĝNS,t er en implisitt estimator på vekstraten til NSt. Den er gitt ved:
(8)
hvor . Parameteren r representerer periodene det tar før en smittet person kan bringe sykdommen videre. For Covid-19 har r = 4 vært ansett som et fornuftig valg. p bestemmer hvor mange «lags» som tas med i estimeringen av vekstraten. Det er vanlig å velge p = 4. Denne operasjonaliseringen referer vi til som R44 i Figur 2. Ved å betrakte utrykkene ovenfor ser vi at R-tallet vil være nær +1 når den målte smitteøkingen er nær null. Når det har vært stor vekst i NS vil R-tallet være høyere enn +1. Negativ endring i antall nye smittede vil gjøre at R-tallet blir mindre enn +1. Dermed vil det beregnede R-tallet variere, nærmest fra dag til dag, så lenge pandemien varer.
Det finnes en litteratur om estimering av Rt,r,p ved hjelp av tidsrekkemetoder, se Harvey og Kattuman (2021) og referansene der. Et R-tall som beregnes ved å bruke en større p, for eksempel p = 7 vil bidra til å stabilisere estimatet på vekstraten. Ytterligere glatting, i form av glidende gjennomsnitt av R4,4 vil stabilisere R-tallet enda mer.
Det kan også beregnes R-tall basert på nye sykehusinnleggelser og det kan da være gode grunner til å sette (r, p) i (6) til andre tall enn (4, 4). På norske data er det praktiske problemer med å anvende (6) på NINLt i stedet for på NSt. Tallene har i perioder vært så lave at beregningen blir temmelig vilkårlig og kan være vanskelig å tolke. For å utnytte den informasjon som ligger data for nye innleggelser, er det nok andre metoder som er bedre egnet. FHI nevner nettopp antallet nye pasienter som én faktor som har stor betydning for det estimerte R-tallet for Norge.
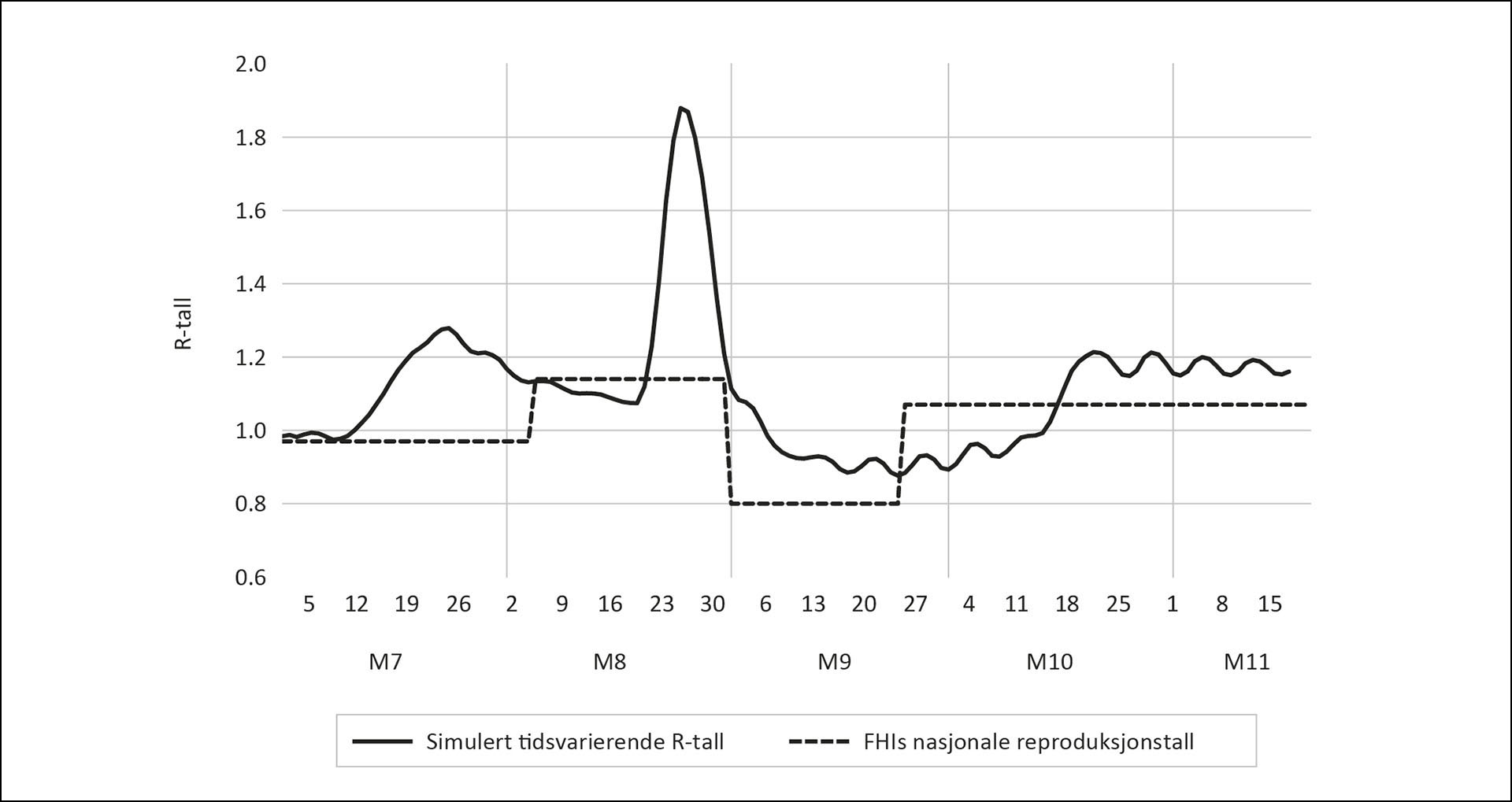
Figur 2: Simulert tidsvarierende R44 fra samme simulering av CovidMod som i Figur 1. Sentrert sju dagers gjennomsnitt. Det nasjonale R-tallet som er estimert av FHI er tatt med som referanse.
Kilde: FHI, Tabell 1 (side 2) i «Situational awareness and forecasting for Norway» datert 5. januar 2022.
Grafen for det simulerte tidsvarierende R-tallet (R44) i Figur 2 ligger nær 1 i starten av simuleringsperioden, og stiger utover i juli. Mot slutten av august viser grafen en markant, men forholdsvis kortvarig økning i det tidsvarierende R-tallet. I september sank det simulerte tidsvarierende R-tallet til litt under 1, før det kom et nytt oppsving mot slutten av oktober som holdt seg i første halvdel av november. Den nasjonale R-tallet som er blitt publisert av FHI er plottet i den stiplede grafen. Vi ser at FHIs estimerte R-tall er konstant i relativt lange perioder. R-tallet ble estimert til å ha vært 0,97 til og med 4. august, og til å ha vært 1,14 resten av den måneden. Det laveste estimatet, 0,8, gjelder for perioden 1. september til 24. september. Fra og med 25. september er det nasjonale R-tallet estimert til 1,07. Det framkommer ikke i Figur 2, men den neste endringen i det nasjonale R-tallet skjedde 13. desember 2021. R-tallet ble da estimert til 0,79.9
Framskrivninger under smittebølgen i november og desember 2021
Etter den kortvarige økning i smitten i august 2021 startet en sterkere og mer varig økning på slutten av oktober, som for øvrig ble reflektert i det tidsvarierende R-tallet i Figur 2. Dette betyr at denne perioden er en interessant «case» for sammenligning av prognosene fra CovidMod med den faktiske utviklingen, slik den ble, og for å sammenligne med FHIs prognoser.
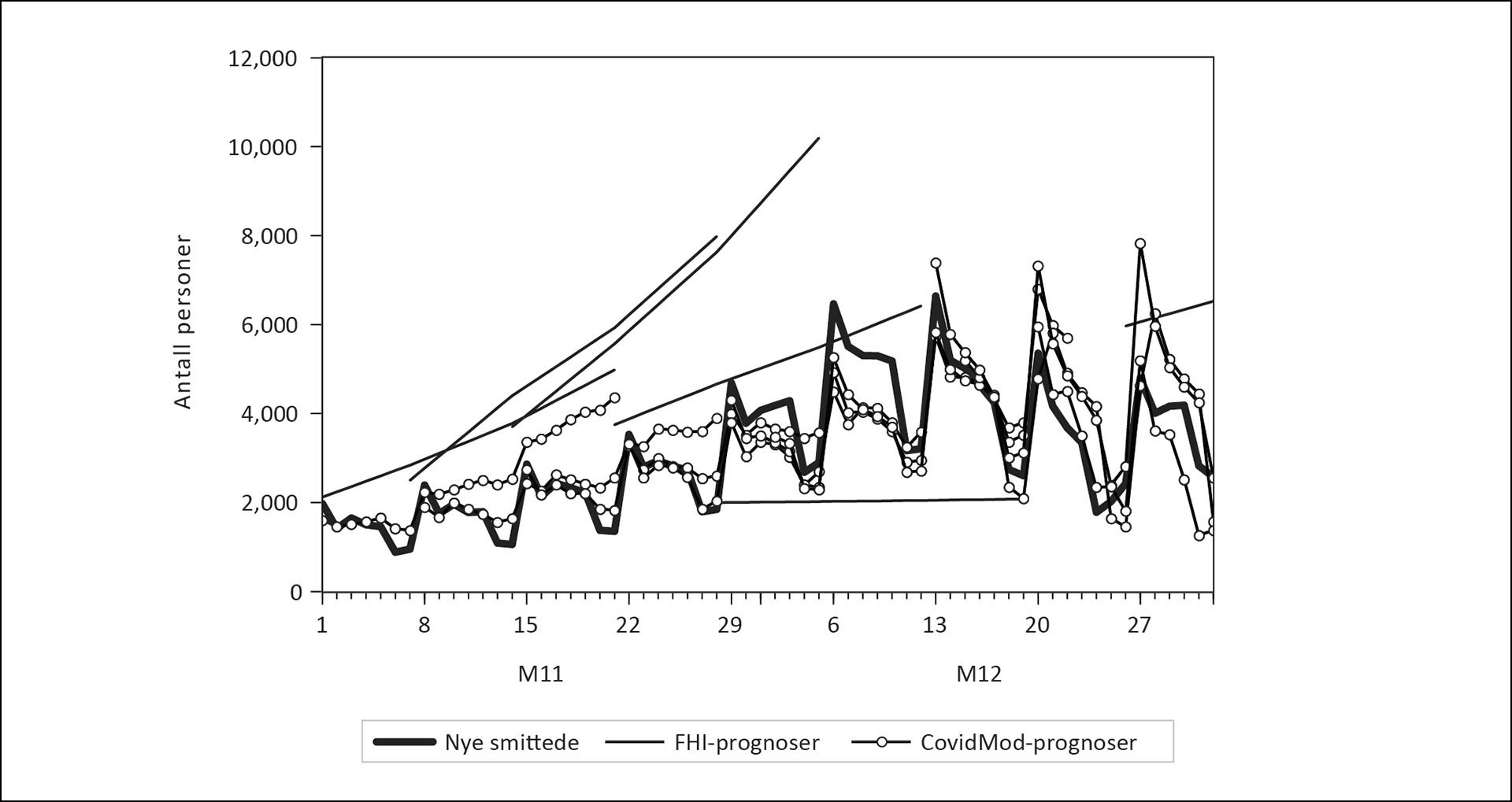
Figur 3: Nye smittede i november og desember 2021, og prognoser fra CovidMod og FHIs National Regional Model.
Kilde: Normetrics, FHI.
I Figur 3 er grafen for faktiske tall for nye smittede tegnet med tykkeste strek. Grafene som er tegnet med tynnere strek angir FHIs prognoser. De viser prognosene i de seks «Situational awareness and forecasting for Norway» rapportene som er datert 3. november, 10. november, 17. november, 24. november, 1. desember og 29. desember. Fordi det er sju dagers mellomrom mellom punktprognosene er det benyttet lineær interpolering for å kunne tegne grafene. Rapportene datert 8.12.21 og 15.12.21 inneholdt imidlertid ikke 21 dagers prognoser for insidens (nye smittede). Dette forklarer hvorfor det er et brudd i sekvensen av grafer med FHI-prognoser. Figuren viser også det settet med CovidMod prognoser som best matcher FHI-prognoser med hensyn til opprinnelsesdato. Disse grafene er merket med symbolet ○.
Prognosegrafene for CovidMod traff nivået på den faktiske smitten forholdsvis godt i den første uken av november. For andre uke blir det tydeligere at data for antall nye smittede ble liggende under tallene i de CovidMod-prognosene som ble laget i starten av måneden.
Prognosene som stammer fra midten av november viser en avmating av smitteveksten i andre halvdel av måneden. Et hovedtrekk er dermed at både CovidMod prognosene, og den faktiske utviklingen, endret seg en god del i løpet av de to første ukene i november. Figur 3 viser at det i starten av desember skjedde en raskere spredning av den registrerte smitten enn det prognosene indikerte ville skje. I den siste perioden som dekkes av figuren, fra 13. desember 2021 til 1. januar 2022, er imidlertid prognosefeilene fra CovidMod igjen noe mindre.
Figur 3 viser at de tre første FHI prognosene indikerte altfor høy smittespredning. Den fjerde FHI-grafen viser at prognosebanen ble betydelig nedjustert fra den forrige prognoserunden. Den femte FHI-grafen er enda mer nedjustert og viser at FHIs prognose i 15. november rapporten var at antall nye smittede ville ligge konstant på omtrent 2000 personer. Dette var ikke noen spesielt god prognose, selv når vi ser bort fra all kortsiktig variasjon i tallene for nye smittede.
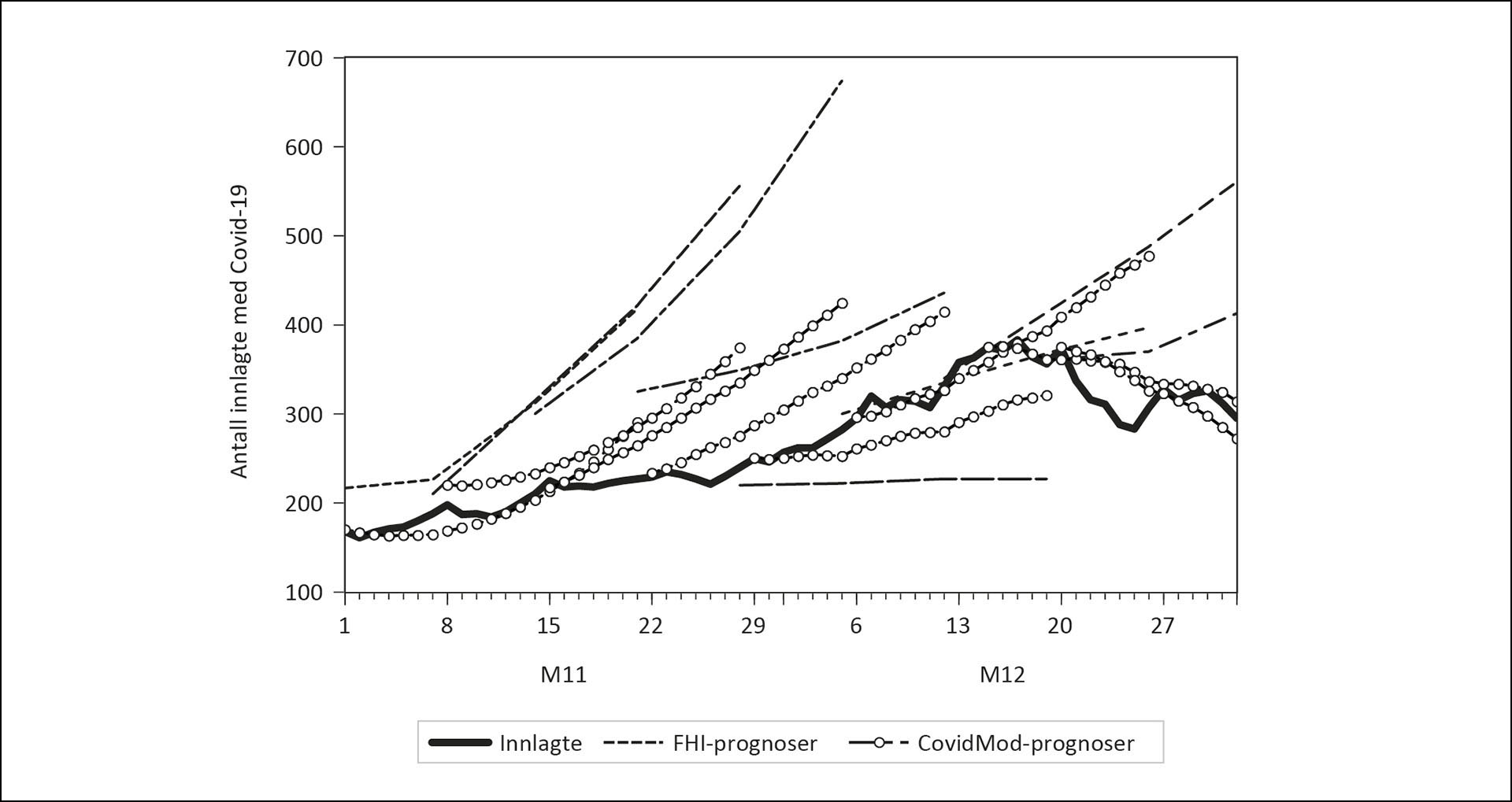
Figur 4: Innlagte på sykehus i november og desember 2021, og prognoser fra CovidMod og FHIs National Regional Model.
Kilde: Normetrics, FHI.
Mot slutten av 2021 ble vurderingen av alvorligheten i pandemien i enda større grad enn tidligere knyttet til antallet pasienter innlagte på sykehus med Covid-19. Figur 4 viser at prognosene for antall innlagte tilsa en økning i behovet for sykesenger. Først fram til slutten av november og siden inn i desember. Antall faktiske innlagte økte mindre enn i prognosene fra midten av november.
De tre første grafene med FHI prognoser ligger vesentlig høyere enn grafene som viser CovidMod prognosene, og dermed også langt over det som ble faktiske tall for innlagte i november. Bemerk den nedjusterte prognosen fra 24. november og ikke minst den lave og flate prognosebanen fra 1. desember (200 innlagte).
Utviklingen i slutten av desember er interessant. Den trendmessige veksten i antall innlagte stoppet opp, og i jula ble det til og med en nedgang i antall innlagte på sykehus med påvist Covid-19. Figur 3 viser at CovidMod traff både trenden og toppunktet bra. De siste tre prognosene fra FHI traff også nivået ganske presist i første del av sine respektive prognoseperioder. Men FHI predikerte ikke den nedgangen i antall innlagte som fant sted i jula.
RMSFE for CovidMod og FHI
I dette avsnittet ser vi på prognosefeilene over en lengre periode: Fra midten av mars 2021 til 19. desember 2021. Over en så lang periode er det upraktisk å basere seg på figurer. Vi ser i stedet på RMSFE («Root Mean Squared Forecast Errors»), som er et standard mål som benyttes ved sammenligning av prognosenøyaktighet. Dette målet legger lik vekt på kvadrert gjennomsnittlig skjevhet i prognosefeilene og variansen til prognosefeilene.
Ved en sammenligning av to prognoser er den prognosen som har lavest RMSFE den optimale prognosemetoden, under visse forutsetninger. En av forutsetningene er at kostnadsfunksjonen av prognosefeil er symmetrisk. Når det gjelder Covid-19 er det imidlertid lett å se for seg at underprediksjon av spredningen av Covid-19 i Norge kan gi spesielt store samlede kostnader hvis pandemien senere slår til for fullt. På den annen side vil det også være kostnader forbundet med å innføre tiltak som senere viser seg å være uforholdsmessige, eller med å vente for lenge med å trappe ned slike ikke-farmasøytiske tiltak. Dette tilsier at det bør knyttes kostnader til både over- og underprediksjoner. Dermed vil sammenligning av RMSFE ha relevans også når det gjelder prognoser av pandemiens utvikling.
Tabell 1 viser RMSFE for nye smittede og for antallet pasienter innlagt på sykehus med Covid-19 diagnose. Den første CovidMod-prognosen stammer fra 19. mars 2021. Den siste som inngår i beregningen er fra 1. november 2021.
FHIs prognoser har som nevnt tre ukers horisont og gjelder insidens (som vi tolker som nye registrert smittede tilfeller) og innlagte, 7, 14 og 21 dager framover i tid fra opprinnelsesdagen til prognosen. Tallene er hentet fra utgaver av «Situational awareness and forecasting for Norway». Det er tallene for gjennomsnitt som er benyttet fordi det gir best sammenligning med prognosene fra CovidMod, som er gjennomsnitt av 1000 stokastiske simuleringer. I tillegg har det vært mulig å avlese hva prognosen for første dag i prognoseperioden er, fra de tilhørende figurene med prognosebaner og usikkerhetsvifter. Dette gir én dag fram prognosene, slik at prognosefeil for h = 1 kan beregnes.
Tabell 1: RMSFE for CovidMod prognosene, med opprinnelsesdato fra 19.3.2021 til 1.12.2021 (CovidMod i tabellen) og FHIs prognoser publisert i de ukentlige modelleringrapportene i løpet av samme tidsperiode, FHI i tabellen.
| Nye smittede | Innlagte | |||
|---|---|---|---|---|
| horisont | CovidMod (n = 178) | FHI (n = 33) | CovidMod (n = 178) | FHI (n = 33) |
| h = 1 | 162, 8 | 897, 15 | 5, 8 | 40, 2 |
| h = 7 | 428, 6 | 1398, 0 | 24, 9 | 52, 6 |
| h = 14 | 629, 9 | 1835, 6 | 46, 1 | 78, 3 |
| h = 21 | 851, 9 | 2400, 6 | 69, 4 | 79, 7 |
Fordi FHI har publisert nye prognoser ukentlig, og ikke alle virkedager, er det færre observasjoner av FHI-prognosefeil, n = 33, enn for CovidMod-prognosefeil, n = 178. Det er derfor knyttet større usikkerhet til RMSFE tallene for FHIs prognoser, enn for CovidMod-prognosene.
Når det gjelder nye smittede viser Tabell 1 at det er markert forskjell mellom RSMFE tallene for CovidMod og FHI. Noe av dette kan nok forklares ved at det ikke er sesongvariasjon i FHI-prognosene, mens det er stor og ganske systematisk variasjon mellom ukedagene i dataene for nye smittede. Det kan selvsagt være god grunn til å se bort fra den helt kortsiktige endringene i smittetallene, siden det er den lokale trenden som sier mer om hvordan smitten brer seg. Men spørsmålet blir da hvilke tall som prognosen egentlig prøver å treffe, hvis det ikke er tallene slik de faktisk ble på framskrivningsdatoen. Forskjellene mellom RMSFE for CovidMod og FHI synes å være større for de korte horisontene enn for de lengre, men også for h = 21 er RMSFE 2,8 ganger høyere for FHI enn for CovidMod.
FHI-prognosene for innlagte har også høyere RMSFE enn CovidMod. Når det gjelder innlagte er det ikke et tydelig sesongmønster, og dermed bidrar ikke dette fenomenet til å forklare forskjellen i prognosenøyaktighet. Bortsett fra den korteste prognosehorisonten er imidlertid de relative forskjellene mellom prognosene mindre for innlagte enn for nye tilfeller.
Avslutning
Når vi arbeider med makroøkonomiske framskrivninger er vi vant til å regne med at strukturelle brudd i økonomien er den viktigste kilden til at store prognosefeil opptrer oftere enn vi skulle ønske. Siden brudd i framskrivningsperioden er uforutsigbare, er det beste man kan håpe på i praksis at de strukturelle bruddene bringes inn i informasjonssettet til prognosemodellene så raskt som mulig etter at de har manifistert seg i data. Prognosemodeller som svikter på dette punktet vil reprodusere framskrivningsfeil, også etter at et strukturelt brudd har funnet sted.
Innenfor samfunnsøkonomi er dette forklaringen på at enkle prognosemodeller, som for eksempel «tilfeldig-gang», ofte kan gjøre det bra sammenlignet med prognoser fra strukturelle modeller. De enkle modellene er ganske riktig naive og de kan bare gi enkle projeksjoner av datatrender. Paradoksalt nok er de likevel mer responsive overfor strukturelle brudd enn det de strukturelle modellene vil være. Dermed vil også prognoser fra strukturelle modeller, som blir korrigert med faktorer fra enklere modeller, kunne gi raskere tilpasning til brudd som har skjedd tett opp mot opprinnelsesdatoen for prognosen. Dette kan tolkes som et eksempel på at det kan være bedre å kombinere prognoser, enn å stole på framskrivningene fra én enkelt prognosemodell.
Det er grunn til å tro at fenomenet strukturelle brudd har vært relevant for Covid-19 prognoser. Det kan samtidig virke som FHI prognosemetoder i stor grad har vært basert på modellering med forholdsvis snevert innslag av empiri i form av anvendte analyser av tidsrekkedata. Dette kan ha gjort prognosene mer utsatt for strukturelle brudd enn de hadde behøvd være. En mer tidsrekkebasert og empirisk modell vil være komplementær til FHIs foretrukne prognosemodell, og ville kunne ha en viss vekt i en litt mer utvidet modellportefølje til overvåkning og framskrivning av epidemien.
Referanser
Bårdsen, G. og R. Nymoen (2014). Videregående emner i økonometri. Fagbokforlaget, Bergen.
Castle, J. L., M. P. Clements og D. F. Hendry (2021). The value of robust statistical forecasts in the Covid-19 pandemic. 11th European Central Bank Conference on Forecasting techniques – Macroeconomic forecasting in abnormal times. 15.–16. juni 2021.
Castle, J. L., J. A. Doornik og D. F. Hendry (2020). Short-term forecasting of the coronavirus pandemic. Antatt for publisering i International Journal of Forecasting.
Harvey, A. C. og P. Kattuman (2021). A Farewell to R: Time series models for tracking and forecasting epidemics. Journal of the Royal Society Interface 18 (182), 20210179. https://doi.org/10.1098/rsif.2021.0179
Nymoen, R. (2019). Dynamic Econometrics for Empirical Macroeconomic Modelling . World Scientific, Boston.
Fotnoter:
- E-post: ragnar.nymoen@econ.uio.no. Beregningene i dette notatet er utført i OxMetrics 8.0/PcGive 15.0 og Eviews 12. Filer med data, estimeringsresultater og prognoser er tilgjengelig på https://normetrics.no/. Under arbeidet med denne artikkelen har jeg hatt nytte av både kritiske og konstruktive kommentarer fra Samfunnsøkonomens anonyme konsulent og fra Lars-Erik Borge. Jeg vil også takke for kommentarer og innspill fra Kåre Bævre, Gunnar Bårdsen, Vegard Lindquist Nymoen, Olav Slettebø og Victoria Sparrman. Norges Forskningsråd prosjektnummer 324472. ↩︎
- Se https://www.fhi.no/sv/smittsomme-sykdommer/corona/koronavirus-modellering/ ↩︎
- https://normetrics.no/covid-19-and-norwegian-jobs-crisis/– innlegget 5-16 May Covid-19 forecast evaluation fra 18. mai 2020. ↩︎
- https://statistikk.fhi.no/msis ↩︎
- https://www.helsedirektoratet.no/statistikk/antall-innlagte-med-pavist-covid-19-for-nedlasting ↩︎
- https://www.fhi.no/sv/smittsomme-sykdommer/corona/dags–og-ukerapporter ↩︎
- Det har variert litt i statistikken om 16.12.2020 eller 17.12.2020 var første dag man satte vaksiner. ↩︎
- CovidMod er i skrivende stund fortsatt en operativ modell. Med nyere data fra pandemien er det estimert effekter av omicron varianten, og av tiltakene fra desember 2021. ↩︎
- Tabell 1 (side 2) i «Situational awareness and forecasting for Norway» datert 5. januar 2022. ↩︎
