Den svake norske kronen – fakta eller fiksjon?¹

Innledning

I løpet av 2017 svekket den norske kronen seg vesentlig mot andre valutaer. I begynnelsen av året kostet en euro nokså nøyaktig 9 kroner. I desember 2017 var kursen 9,84, altså en depresiering på 10 prosent.² Dette kom overraskende på norske økonomer (Dagens Næringsliv, 3. januar 2018). I gjennomsnitt hadde de forventet at kronen skulle styrke seg (appresiere) mot euro gjennom 2017, til en verdi på 8,83. Men en sjeføkonom som ble intervjuet tilskrev dette midlertidige faktorer, særlig en urealistisk forventing i markedet om kollaps i det norske boligmarkedet. Derfor regnet han med at kronen ville appresiere kommende år og anslo at en euro ville koste 8,80 ved slutten av 2018. Gjennomsnittskursen for desember 2018 endte på 9,79. Dette bildet gjentok seg året etter. I januar 2019, da kursen i gjennomsnitt var 9,76, ble 11 sjeføkonomer intervjuet om sine valutaprognoser (Finansavisen, 4. januar 2019). De regnet alle med at kronen ville styrke seg i løpet av 2019. De fleste anslo at eurokursen ville bli mellom 9,00 og 9,30. Det ble en ny skivebom.³ Gjennomsnittet for desember 2019 ble 10,05.

I tre år på rad bommet altså norske økonomer grovt på kronekursen, alle ganger i samme retning. At økonomer ikke er i stand til å gi prognoser for valutakursen som slår myntkast, er ikke overraskende i lys av den velkjente artikkelen til Meese og Rogoff (1983) og nyere undersøkelser av norske bankers valutaprognoser.⁴ Dette er ikke hovedpoenget her. Det som er overraskende, er at det i 3 år var en vedvarende tro på at svekkelsen av kronekursen var midlertidig og at eurokursen ville vende tilbake til nivåene før 2017. Dette tyder på at valutaanalytikerne hadde oversett at en viktig driver for valutakursen hadde endret seg. Det er den vi er på jakt etter i denne artikkelen.

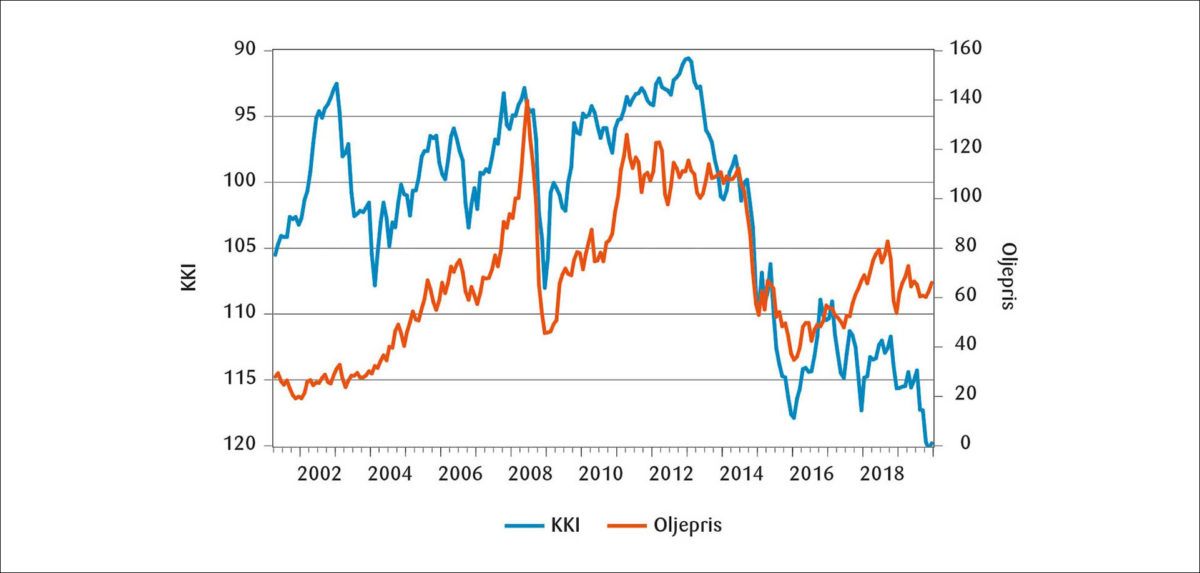
Utviklingen i kronekursen og faktorer som påvirker den

Svekkelsen av kronekursen gjennom 2015 og 2016 gikk sammen med en betydelig nedgang i oljeprisen (se figur 1). Vi bruker her, og i det følgende, konkurransekursindeksen (KKI) som mål på valutakursen.⁵ Det er grundig dokumentert i tidligere studier at oljeprisen har en signifikant innflytelse på NOK. Akram (2019) fant at en økning i oljeprisen på 10 prosent ga en appresiering av kronen på 0,8 prosent, som er på linje med estimatet på 0,6 prosent i Bernhardsen (2008). Men oljeprisen tok seg opp igjen i 2018 uten at kronen løftet seg, så den kan ikke alene forklare den svake kronekursen i de senere år.

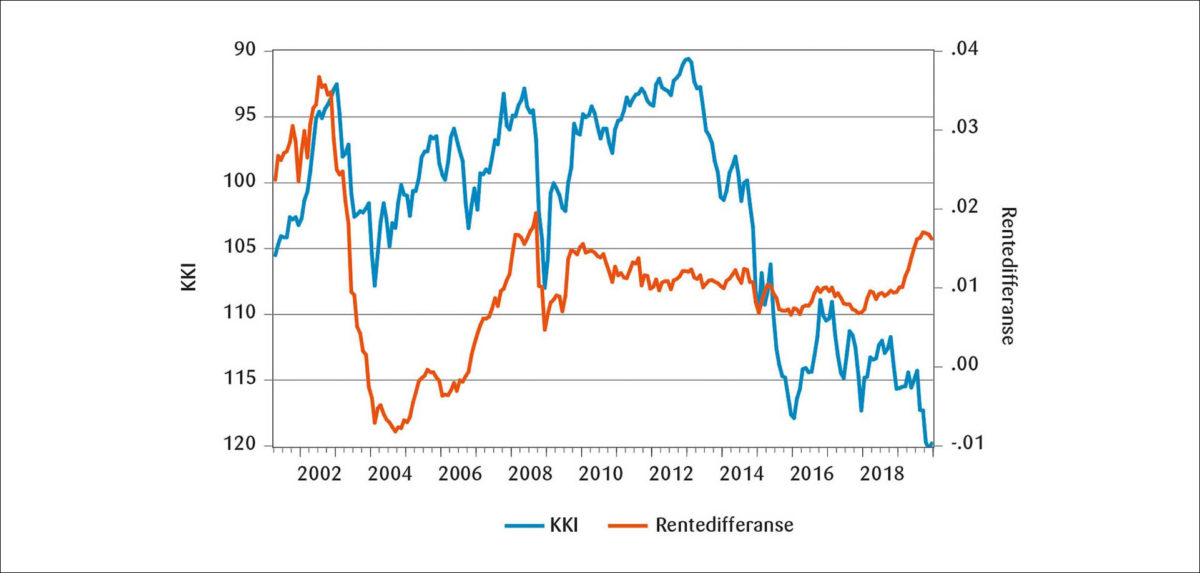
Rentedifferansen mot utlandet tillegges av mange stor betydning for valutakursutviklingen. Enhver potensiell renteøkning fra Norges Banks side blir møtt med kraftige advarsler om at det vil føre til en vesentlig styrking av kronen. Det er nokså entydig belegg i tidligere empiriske studier av NOK at renten har en klar signifikant, men likevel relativt moderat effekt på kronekursen. En økning i rentedifferansen på 1 prosentpoeng (som ville vært en kraftig pengepolitisk innstramming i Norge) gir ifølge flere studier en appresiering av kronen på rundt 3 prosent.⁶ Figur 2 viser utviklingen i en vektet differanse for 12 måneders pengemarkedsrenter mot utlandet og KKI.⁷ Etter finanskrisen i 2008 har denne størrelsen ligget nokså stabilt på rundt 1 prosentpoeng, mens valutakursen har beveget seg i lange svingninger, fra indeksverdier rundt 90 i 2013 til 120 i 2019. Bjørnstad og Jansen (2006) valgte tittelen «Renta bestemmer det meste» for sin valutakursmodell, som nok er inspirert av samvariasjonen i årene 2001–2003. En inspeksjon av figuren tyder derimot på at rentedifferansen ikke kan ha hatt vesentlig betydning for valutakursutviklingen i årene etter finanskrisen, siden den har vært veldig stabil i lange perioder. Det er vanskelig å se for seg at «renta bestemmer det meste» ut fra forløpet til rentedifferansen (vist i figur 2) i årene etter dette.

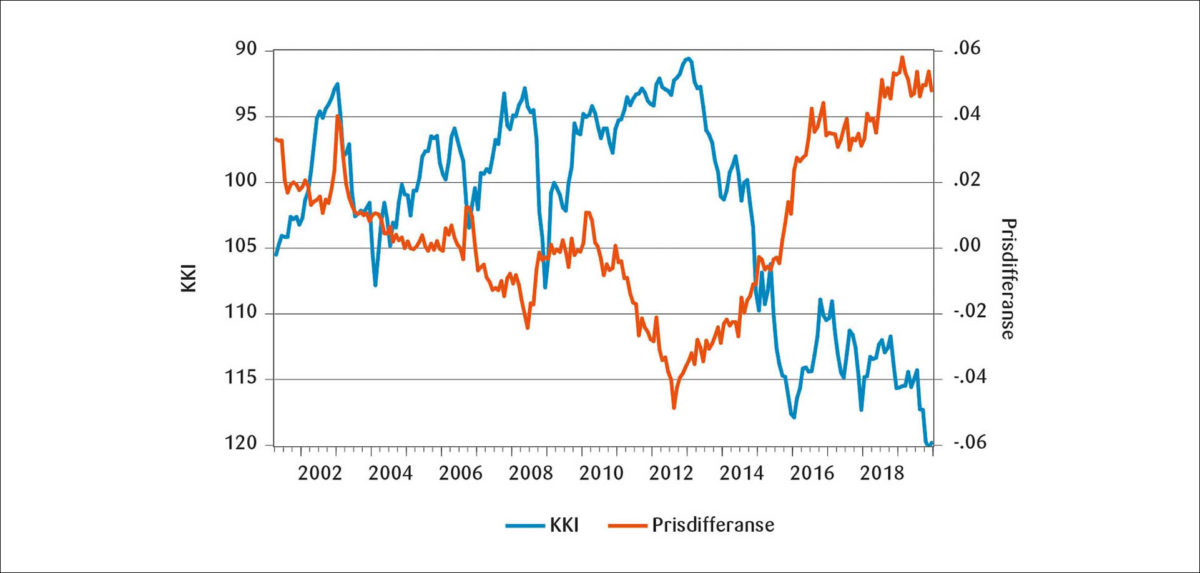
Både oljeprisen og rentedifferansen mot utlandet hører hjemme i en modell for NOK-kursen, men gir ikke noen tilstrekkelig forklaring på kronesvekkelsen de siste årene. En faktor som i perioder har hatt stor betydning, er internasjonal finansuro. Under finanskrisen i 2008–2009 svekket NOK seg kraftig. Eurokursen endret seg på kort tid fra 8 til 10 kroner, og vi ser et brått men relativt kortvarig fall i indeksverdien for NOK. Det er velkjent at i tider med finansiell ustabilitet søker aktørene til trygge havner, hvor det er dype verdipapirmarkeder. Flatner (2009) finner blant annet at den norske kronen ikke fungerte som en trygg havn-valuta under finanskrisen, men snarere det motsatte, fordi det samtidig fant sted en kraftig depresiering av kronen. Det blir for trangt i døren når finansaktørene skal ut av NOK på kort varsel. Siden den gang har flere episoder med internasjonal finansiell uro påvirket kronekursen, men det har vært i korte perioder og kan derfor ikke forårsake en vedvarende kronesvekkelse.

Vi ser av figurene ovenfor, at KKI-indeksen beveget seg fra verdier rundt 95 i årene før 2014, til rundt 115 fra og med 2016. Eurokursen gikk fra et nivå på mellom 8 og 9 kroner per euro, til å ligge mellom 10 og 11 kroner. Det tilsvarer en kronedepresiering på ca. 20 prosent. Vi mener at vi har funnet en viktig kilde til dette. Den ligger i den relative prisutviklingen i Norge og utlandet. Figur 3 viser utviklingen i differansen mellom harmonisert prisindeks for Norge og utlandet, oppgitt på logaritmisk form.⁸ Det som er mest interessant å merke seg her, er at mens prisnivået for utlandet lå over det norske noen år etter finanskrisen, så snudde dette rundt 2015, og Norge fikk en betydelig høyere prisvekst enn utlandet.⁹ At valutakursen da vil depresiere, er hva den velkjente teorien om relativ kjøpekraftsparitet vil si. Alt annet like, impliserer denne teorien at valutakursen vil endre seg proporsjonalt med prisnivådifferansen mellom hjemland og utland. Vårt første skritt i den empiriske analysen blir å teste om denne teorien alene kan forklare svekkelsen av kronekursen.

Tabell 1: Univariat modell av den norske realvalutakursen (q)

∆qt^=0.121-0.026qt-1+0.233Δqt-1-0.139Δqt-2​  ( 0.077 ) ​   ​ ( 0.017 ) ​        ​(0.067)​           (0.068)​
Estimeringsperiode: 2001M7-2020M1: T = 223
t-ADF = -1.566, DF-kritiske verdier:		1%:	-3.469
R2  = 0.070		5%:	-2.882
		10%:	-2.572
Vekter p*: EUR(52.5%), SEK(16%), GBP(14.2%), USD(8.7%), PLN(4.4%), JPY(2.2%), CAD(2%)
Diagnostiske tester
Standardavvik residualer:	σ^e	=	0.0143
AR, 1-2	F(2,217)	=	0.748 [0.4747]
ARCH 1-2	χ2(2)	=	4.981 [0.0829]*
Normalitetstest	χ2(2)	=	11.180 [0.0037]***
Skjevhet			0.4626
Kurtose – 3			0.8729
Spesifikasjonstest, RESET	F(3,216)	=	2.58 [0.0545]*

En test for kjøpekraftsparitet

Hvis kjøpekraftsparitetshypotesen holder eksakt, vil den nominelle valutakursindeksen (s) endre seg i takt med prisdifferansen mellom hjemland og utland (p – p^*). Det impliserer at den reelle valutakursen q, somer definert ved

q =  s – p + p^*     (1)

er konstant over tid (her er alle variabler på log-form). I empiriske tester godtar vi hypotesen hvis q er en stasjonær tidsserie.¹⁰

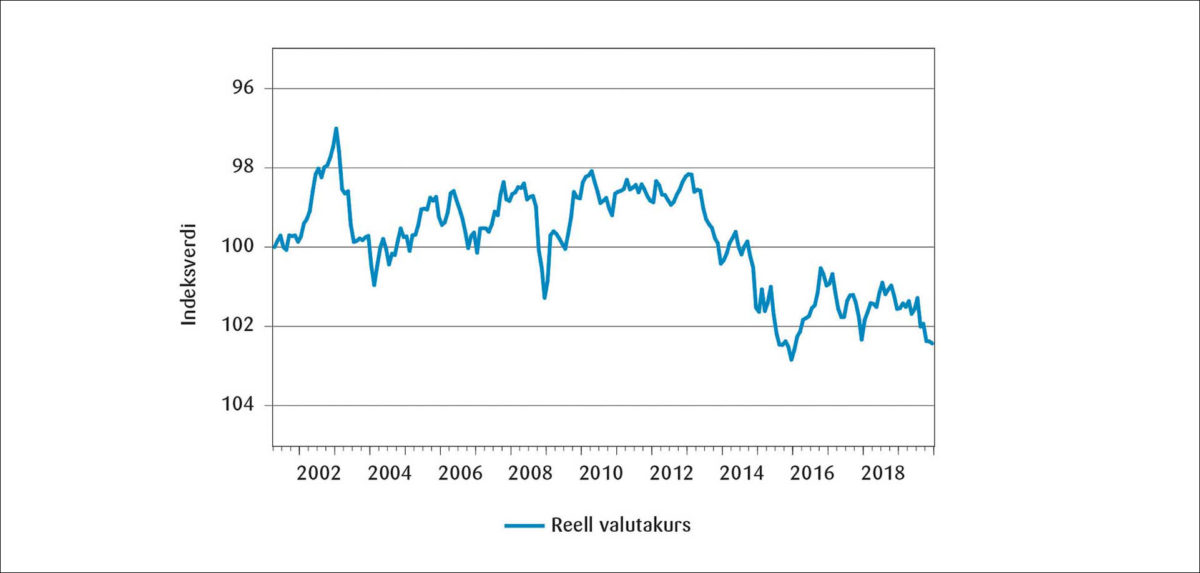
Figur 4 viser utviklingen av den reelle valutakursindeksen over tid. Den viser at prisdifferansen i lange perioder ser ut til å fange opp en god del av valutakurssvingningene, idet indeksen frem til 2014 stort sett bare beveger seg inntil et par prosent fra utgangspunktet. Dette bildet er veldig forskjellig fra de store fluktuasjonene i den nominelle valutakursen i figur 1, som beveget seg med 10 prosent i hver retning fra utgangspunktet. Men det er et tydelig skift til en svakere realkurs etter 2014, som tyder på at kjøpekraftsparitetshypotesen ikke holder eksakt over hele perioden.

Vi har benyttet Augmented Dickey Fuller test (ADF) for enhetsrot, gjengitt i tabell 1. Estimeringsperioden er satt fra juli 2001 til januar 2020, noe som tilsier 223 observasjoner og en periode med samme pengepolitisk regime, altså inflasjonsstyring. Antall lags er valgt ved å starte med 12 lags og benytte general-to-specific metode, beskrevet i Enders (2015). 

De diagnostiske testene viser at vi kan beholde nullhypotesen om ingen autokorrelasjon i residualene opptil 2.orden. ARCH-testen viser også at vi kan beholde nullhypotesen om ingen autokorrelasjon i varians til residualene opptil 2.orden, på 5 prosent nivå. Selv om vi må forkaste hypotesen om normalitet i residualene, ser vi at både skjevhet og kurtose-3 holder seg innenfor +/- 1, noe som indikerer at de er rimelig normalfordelte.¹¹ Nullhypotesen om ingen utelatte variabler kan beholdes marginalt utenfor 5 prosent nivå.

Testen bekrefter vår antagelse om at vi ikke kan forkaste nullhypotesen om ikke-stasjonaritet. Den enkle kjøpekraftsparitetshypotesen er ikke tilstrekkelig til å forklare valutakursutviklingen. Vi må derfor gå videre til en utvidet modell for valutakursen som omfatter faktorer som oljepris, rentedifferanse og finansiell risiko.

En modell for den norske kronen

Basert på diskusjonen ovenfor har vi konstruert en vektor feiljusteringsmodell, hvor vi undersøker om kronekursen har beveget seg omkring en modellert fundamentalverdi. Vi finner såkalt «feilkorreksjon», noe som vil si at kronekursen vender tilbake mot fundamentalverdien i de tilfellene det har vært avvik mellom disse i forrige periode. Vi benytter konkurransekursindeksen (kki) som avhengig variabel. Modellen inneholder forklaringsvariablene oljepris, rentedifferanse  (i¹²-i^*12), Prisdifferanse  (p-p^*), risikoindikatoren CVIX og indeksen S&P500. 

Oljeprisen, representert ved Brent Blend, har historisk sett vært en viktig variabel for å modellere kronekursen. Siden mye av Norges inntekter er basert på salg av olje, vil oljeprisen spille en stor rolle for inntektene til Norge. Rentedifferansen er tolvmåneders nominell pengemarkedsrente i hjemlandet, fratrukket en tilsvarende rente for utlandet. Prisdifferansen mellom hjemlandet og utlandet er konstruert med basis i harmonisert konsumprisindeks (HKPI), som er en felles målestokk for prisnivå i de respektive landene. Prosentvektene vi har benyttet for å beregne rentedifferanse og prisdifferanse for utlandet, er Euro-området (52,5), Sverige (16), Storbritannia (14,2), USA (8,7), Polen (4,4), Japan (2,2) og Canada (2). Selv om det hadde vært ideelt å benytte renter og tilhørende vekter for alle de 25 viktigste handelspartnerne, er gevinsten ved å gjøre dette svært liten for det totale aggregatet. 

Risikoindikatoren vi har valgt å benytte har som hovedformål å måle effekten av uro i finansmarkedene på kronekursen. CVIX (Deutsche Bank’s currency volatility index) er en global risikoindikator som måler markedets forventede fremtidige volatilitet for de 9 største valutaparene. CVIX er beregnet ved å benytte et aritmetisk snitt av prisene på 3 måneders valutaopsjoner. Den norske kronen oppfattes ofte som en liten og perifer valuta, og ved større usikkerhet i markedene vil kronen merke effekten av at investorer rømmer til trygge havner. Den siste variabelen som er inkludert i modellen, er S&P 500, som måler markedsverdien til de 500 mest omsatte aksjeselskapene ved børsene NYSE og NASDAQ. Formålet med variabelen er å vise at utsikter til høyere avkastning i det amerikanske aksjemarkedet fører til at investorer trekker midler ut av en liten valuta som den norske kronen, og plasserer det i aksjer i USA. Denne variabelen var for øvrig også med i den første modellen til Norges Bank (Naug, 2003).

Langtidsdynamikk

For å finne en langtidsmodell for den norske kronen, har vi benyttet ulike kombinasjoner av en rekke forklaringsvariabler, og testet modellene for kointegrerte forhold.¹² Den foretrukne modellen gir ett kointegrert forhold, og med én kointegrert vektor og seks variabler, finner vi følgende ​Π​ – matrise, beskrevet i Brooks (2019):

$\Pi =\alpha \beta ´=\left(\begin{array}{c}{\alpha }_{11}\left(kki\right)\\ {\alpha }_{12}\left(i^{12}–i^{*12}\right)\\ \begin{array}{c}{\alpha }_{13}\left(p–p^{*}\right)\\ {\alpha }_{14}\left(oljepris\right)\\ \begin{array}{c}{\alpha }_{15}\left(cvix\right)\\ {\alpha }_{16}\left(s\&p500\right)\end{array}\end{array}\end{array}\right)$

$\left(\begin{array}{c} \\ \begin{array}{ccc}{\beta }_{11}\left(kki\right),& { \beta }_{12}\left(i^{12}–i^{*12}\right),& \begin{array}{cc}{ \beta }_{13}\left(p–p^{*}\right),& \begin{array}{cc}{\beta }_{14}\left(oljepris\right),& \begin{array}{cc}{\beta }_{15}\left(cvix\right),& {\beta }_{16}\left(s\&p500\right)\end{array}\end{array}\end{array}\end{array}\\ \end{array}\right)$

$= \left(\begin{array}{c}{\alpha }_{11}\left(–0.102\right)\\ {\alpha }_{12}\left( 0.014\right)\\ \begin{array}{c}{\alpha }_{13}\left( 0.037\right)\\ {\alpha }_{14}\left(–0.570\right)\\ \begin{array}{c}{\alpha }_{15}\left( 0.246\right)\\ {\alpha }_{16}\left( 0.112\right)\end{array}\end{array}\end{array}\right)$

$\left(\begin{array}{c} \\ \begin{array}{ccc}{\beta }_{11}\left(1\right),& { \beta }_{12}\left(1.462\right),& \begin{array}{cc}{ \beta }_{13}\left(–0.863\right),& \begin{array}{cc}{\beta }_{14}\left(0.081\right),& \begin{array}{cc}{\beta }_{15}\left(–0.112\right),& {\beta }_{16}\left(–0.169\right)\end{array}\end{array}\end{array}\end{array}\\ \end{array}\right)$     (2)

Modellen er estimert uten restriksjoner, og de estimerte verdiene er oppgitt i parentes. Matrisen β uttrykker kointegrasjonsvektorene, mens α uttrykker justeringsparameterne. Ved å presentere betavektoren på denne måten, er det viktig å legge merke til at de estimerte koeffisientene inngår med motsatt fortegn. Lengre ned i artikkelen, hvor vi har presentert den endelige langtidsløsningen, har vi løst ut kki på venstre side og presentert koeffisientene med riktig fortegn. Justeringsparameterne måler hastigheten på feiljusteringsmekanismen, noe som vil si hvor lang tid systemet bruker på å reverseres tilbake til likevekt (Wang, 2003).

Tabell 2: Testresultater for restriksjoner på langsiktig kointegrasjonsvektor (β).

${\beta }_{11}\left(kki\right)+{ \beta }_{12}\left(i^{12}–i^{*12}\right) +{ \beta }_{13}\left(p–p^{*}\right) +{ \beta }_{14}\left(oljepris\right) + {\beta }_{15}\left(cvix\right) + {\beta }_{16}(s\&p500)$
Hypotese	Restriksjoner	Estimert beta	Test statistikk	[p-verdi]
H 1 : Ren PPP	(1, 0, -1, 0, 0, 0)	(1, 0, -1, 0, 0, 0)	${\chi }^2\left(5\right)=28.46$	[0.00]***
H 2 : Utvidet PPP 1	(1, 0, -1, *, 0, 0)	(1, 0, -1, 0.149, 0, 0)	${\chi }^2\left(4\right)=14.41$	[0.01]***
H 3 : Utvidet PPP 2	(1, 0, -1, *, *, 0)	(1, 0, -1, 0.220, -0.243, 0)	${\chi }^2\left(3\right)=9.37$	[0.02]**
H 4 : Tvungen PPP	(1, *, -1, *, *, *)	(1, 1.462, -1, 0.077, -0.110, -0.161)	${\chi }^2\left(1\right)=0.213$	[0.65]

Notat: Utvidet PPP 1 er kjøpekraftsparitet med fritt vandrende oljepris, mens utvidet PPP 2 er kjøpekraftsparitet med fritt vandrende oljepris og risikoindikator. Under kolonnen for restriksjoner, indikerer * at koeffisienten får vandre fritt i estimeringen, mens under kolonnen for p-verdi er tilsvarende relatert til signifikansnivå: ***1% signifikansnivå, **5% signifikansnivå, *10% signifikansnivå.

Restriksjoner

Det er mulig å teste ulike varianter av kjøpekraftsparitet ved å sette restriksjoner på betavektoren, og dermed teste relasjonene i et system. Dette gir oss også muligheten til å se hvordan de øvrige koeffisientene reagerer på restriksjonene. I tabell 2 benytter vi en likelihood-ratio test for å teste nullhypotesen om at restriksjonene er gyldige.¹³ Ikke overraskende må vi også her forkaste hypotesen ( H₁) om ren kjøpekraftsparitet. Vi tester videre en utvidet kjøpekraftsparitet ( H₂) med realøkonomiske sjokk, hvor oljeprisen dermed får vandre fritt i modellen. Vi ser at p-verdien øker noe, men at også denne hypotesen må forkastes på 1%-nivå.

Ved å utvide kjøpekraftspariteten ytterligere ( H₃), slik at både oljepris og risikoindikatoren vandrer fritt i estimeringen, finner vi en ytterligere økning i p-verdien, men at denne må forkastes på 5%-nivå. Vi kan med andre ord avvise ren kjøpekraftsparitet og utvidelser av denne, ved å teste relasjonene i et system.

Vi har i tillegg estimert en modell ( H₄) hvor vi pålegger den foretrukne modellen å følge relativ kjøpekraftsparitet, samtidig som alle andre koeffisienter får vandre fritt. Her er ikke poenget å anse dette som en utvidelse av kjøpekraftsparitet, men heller å se hvordan de andre koeffisientene reagerer på restriksjonen. Ved å pålegge modellen å følge en mer teoretisk riktig spesifikasjon, observerer vi at koeffisientene holder seg tilnærmet like som for den opprinnelige modellen uten restriksjon.

For å teste om enkeltvariablene responderer på avvik fra den langsiktige likevektsrelasjonen, setter vi enkeltvise restriksjoner på alfavektoren fra  Π-matrisen presentert ovenfor. Vi benytter en likelihood-ratio test for å teste om variablene er svakt eksogene, noe som vil si at vi ikke kan forkaste at hastigheten på den enkelte justeringsparameteren er lik 0 (Enders, 2015).

Tabell 3: Testresultater for restriksjoner på justeringsparameterne (α).

${\alpha }_{11}\left(kki\right) +{ \alpha }_{12}\left(i^{12}–i^{*12}\right) +{ \alpha }_{13}\left(p–p^{*}\right) +{ \alpha }_{14}\left(oljepris\right) + {\alpha }_{15}\left(cvix\right) + {\alpha }_{16}(s\&p500)$
Variabel	Restriksjoner	Estimert alfa	Test statistikk	[p-verdi]
Uten restriksjon	(*, *, *, *, *, *)	(-0.10, 0.01, 0.04, -0.57, 0.25, 0.11)	–	–
Null respons kki	(0, *, *, *, *, *)		${\chi }^2\left(1\right)=3.28$	[0.07]*
Null respons  $\left(i–i^{*}\right)$	(*, 0, *, *, *, *)		${\chi }^2\left(1\right)=5.63$	[0.02]**
Null respons  $\left(p–p^{*}\right)$	(*, *, 0, *, *, *)		${\chi }^2\left(1\right)=6.68$	[0.01]**
Null respons oljepris	(*, *, *, 0, *, *)		${\chi }^2\left(1\right)=3.62$	[0.03]**
Null respons cvix	(*, *, *, *, 0, *)		${\chi }^2\left(1\right)=0.65$	[0.42]
Null respons s&p500	(*, *, *, *, *, 0)		${\chi }^2\left(1\right)=0.85$	[0.36]

Tabell 3 viser at vi kan forkaste nullhypotesen om svak eksogenitet for rentedifferanse, prisdifferanse og oljepris på 5%-nivå, mens KKI kun kan forkastes på 10%-nivå. Vi kan ikke forkaste nullhypotesen for CVIX og S&P 500, noe som gjør at variablene fremstår som svakt eksogene.

Ved å se på fortegnene til alfakoeffisientene, kan vi se om de enkelte bidrar til å føre feiljusteringen mot likevekt. Alfakoeffisientene sier videre noe om variablenes respons i de tilfellene KKI avviker fra sin fundamentalverdi. Fortegnene kan også evalueres ved å undersøke om responsen gir mening i forhold til økonomisk teori.  α11bidrar i riktig retning i det den forventes å være negativ. Intuisjonen er at, i de tilfellene kronekursen er svakere enn det fundamentalverdien tilsier, så skal den styrke seg mot sin langtidssammenheng. Det vil si at den skal bli mer negativ, ettersom en lavere verdi tilsvarer en sterkere krone.  α₁₂ bidrar også i riktig retning, i det den er positiv. Ved en svak kronekurs i forhold til fundamentalverdien, er en mulig tolkning at konkurranseevnen mot utlandet bedres, noe som normalt tilsier økt nettoeksport. I tillegg vil import bli mindre attraktivt, og vi får en vridning over til norske varer. En siste effekt, er at en svak krone medfører at importere varer blir dyrere. Isolert sett, tilsier dette høyere importert prisvekst, ettersom importens andel av konsumprisindeksen utgjør om lag 30 prosent. Totalt sett vil dette på sikt bidra til høyere inflasjon og en kontraktiv pengepolitikk ved høyere innenlands rente. Isolert sett vil dette tilsi en økt rentedifferanse mot utlandet, og derav riktig fortegn på alfakoeffisienten.  α₁₃ er også positiv, noe som vil si at den har riktig fortegn. Her er intuisjonen at en for svak krone i forhold til fundamentalverdien vil føre til en økning i prisnivået, noe som er konsistent med fortolkningen av  α₁₂.

Det vil ikke være rimelig å anta at  α₁₄,  α₁₅ og  α₁₆ skal respondere på avvik i den norske kronekursen. Poenget er at den norske kronen har for liten gjennomslagskraft i den internasjonale økonomien til at det vil være rimelig å anta at internasjonale variabler som oljepris, CVIX og S&P500 skal respondere på kronens avvik fra dens langtidssammenheng. Vi har derfor gått videre i utredningen med å sette nullrestriksjoner på disse alfakoeffisientene, noe som vil si at de blir hindret i å respondere på feiljusteringsleddet.

Langtidsløsning

Med nullrestriksjoner på ${\alpha }_{14}$, ${\alpha }_{15}$ og ${\alpha }_{16}$i alfavektoren fra likning 2, estimerer vi en ny betavektor som danner grunnlag for feiljusteringsleddet. Ved å omrokere variablene i feiljusteringsmodellen, får vi følgende langtidsmodell for KKI:

$kki= 3.4869 –\begin{array}{c}1.5347\left(i^{12}–i^{*12}\right)\\ \text{(0.4099)} \end{array}$

$+\begin{array}{c}1.0238\left(p–p^{*}\right)\\ \text{(0.2564)} \end{array}–\begin{array}{c}0.0590\left(oljepris\right)\\ \text{(0.0123)} \end{array}$

$+ \begin{array}{c}0.0878\left(cvix\right)\\ \text{(0.0180)} \end{array}+\begin{array}{c}0.1637\left(s\&p500\right)\\ \text{ (0.0175)} \end{array}$     (3)

For en grafisk illustrasjon, har vi plottet langtidsløsningen opp mot KKI i figur 5. Ved å observere figuren, gir det et innblikk i hvor godt feiljusteringen følger kronekursutviklingen. Det er tydelig at tidsseriene følger hverandre rimelig tett, men at modellen faller noe sammen mot slutten av estimeringsperioden. Spesielt for de siste månedene av 2019 ser modellen ut til å indikere feil retning, og dermed også feil nivå. For øvrig forklarer modellen 90 prosent av den faktiske utviklingen til KKI. Ved å benytte disse variablene til å forklare kronens fundamentale nivå, ser vi at feiljusteringen ikke avviker særlig fra det faktiske nivået til KKI i perioden etter oljeprisfallet. Et nivå som gjennomsnittlig har fluktuert rundt 115. Vi ser likevel betydelige kortsiktige avvik fra dette nivået i slutten av både 2016 og 2019.

En fortolkning av koeffisienten til rentedifferansen tilsier at en økning i rentedifferansen på 100 basispunkter gir en reduksjon av KKI på omtrentlig 1,5 prosent, noe som vil si en appresiering av kronekursen. Det er litt lavere enn andre studier referert ovenfor, men effekten vil kunne avhenge av hvilke renter som benyttes. Dette resultatet viser at den langsiktige renteeffekten på valutakursen er relativt liten. Vi har valgt 12 måneders pengemarkedsrenter, som hos Bernhardsen (2008). Dette vil kunne fange opp noe mer langsiktige renteforventninger enn 3 måneders renter. Det kan være av betydning ettersom Johansen og Pedersen (2017) viste at også Norges Banks rentebane har betydning for kronekursen.

I henhold til teori om kjøpekraftsparitet skal koeffisienten til prisdifferansen være 1. Modellen estimerer en koeffisient som er veldig nær dette (1,02). En økt prisdifferanse gir dermed en økning i KKI, noe som vil si en depresiering av kronen. Den estimerte langtidsrelasjonen viser at man kan omdanne ligningen til å forklare den reelle valutakursen uten store endringer i koeffisientestimatene.

En økt oljepris har historisk sett styrket kronen. Dette stemmer også i vår modell, hvor en økning i oljeprisen på 10 prosent fører til en appresiering av kronekursen på omtrentlig 0,6 prosent. Det er ofte to nevnte årsaker til at oljeprisen påvirker kronekursen. Den første går ut på at økt oljepris øker verdien av oljerelaterte selskaper på Oslo Børs. Oljeselskaper har historisk utgjort en stor andel av Oslo Børs, men det er verdt å merke seg at denne andelen er blitt redusert de senere årene. Utenlandske investorer vil i neste omgang investere i disse selskapene, og må dermed kjøpe norske kroner. Den økte etterspørselen etter norske kroner bidrar til en appresiering av kronen. Den andre grunnen, er at økt oljepris øker statens inntekter, noe som i utgangspunktet skal gi en appresierende effekt på kronen.

CVIX forklarer hvordan uro i valutamarkedene påvirker kronekursen. Modellen estimerer en koeffisient på 0,088 for denne variabelen, noe som vil si at økt volatilitet i valutamarkedene fører til depresiering av kronekursen. Fortegnet er dermed som forventet, da den norske kronen ikke betraktes som en trygg havn. Dette vil i praksis bety at når volatiliteten i markedet øker, så vil investorer selge kroner for å kjøpe valuta som ansees som et tryggere alternativ.

Den siste variabelen i modellen, er den amerikanske aksjeindeksen S&P 500. Variabelen estimeres med positivt fortegn. Grunnen til at kronen svekkes av en økning i amerikanske aksjer på lang sikt, kan blant annet knyttes mot at investorer ønsker å ta del i den økonomiske oppgangen i USA. Dette medfører at de flytter investeringer over til det amerikanske aksjemarkedet og dermed er avhengig av å kjøpe dollar. Isolert sett vil kjøp av dollar for norske kroner gi et depresieringspress på den norske kronen.

Ut fra fortegnene til variabelkoeffisientene, er modellen i tråd med hva vi kan forvente fra økonomisk teori og intuisjon. Ved å benytte denne analysen i en kombinasjon med en grafisk fremstilling av variablene, er det mulig å diskutere hvorfor modellen estimerer et fundamentalnivå som er rimelig i tråd med den faktiske kronekursen i perioden 2017–2020. Fram til 2019 har rentedifferansen vært rimelig stabil, mens det har vært en økning etter dette. Oljeprisen har økt i perioden, fra rundt 35 til stabilt over 60 dollar per fat. Isolert sett, tilsier disse økningene en appresiering av kronen etter 2016. CVIX på sin side, har hatt liten endring denne i perioden. S&P 500 har økt, men mer fundamentalt vil det være å se på økningen i prisnivådifferansen mot utlandet. Denne økningen tilsvarer en relativt betydelig depresiering i perioden (kfr. figur 3), og er med på å utligne effekten fra oljepris og rentedifferanse. Dette er noe som kan være med på å forklare hvorfor modellen estimerer et fundamentalnivå omkring faktisk kronekurs.

Korttidsdynamikk

Korttidsdynamikken baserer seg på den laggede feiljusteringsmekanismen, kombinert med forklaringsvariabler på differanseform som ut ifra økonomisk teori kan påvirke kronekursen på kort sikt. Forklaringsvariablene som inngår i langtidsmodellen, er også inkludert i laggede utgaver ved estimering av korttidsmodellen. Ved å benytte en general-to-specific metode, finner vi følgende korttidsmodell for kronekursen:

En positiv ${∆kki}_t$indikerer en depresiering av kronekursen og modellen forklarer 35,8 prosent av endringene i KKI, målt ved justert R-kvadrat $\left({\bar{R}}^2\right)$ . Den positive koeffisient for ${∆\left(kki\right)}_{t–1},$impliserer at alt annet like, vil en depresiering (appresiering) av KKI forrige måned på 1 prosent, gir en svekkelse (styrking) av kronekursen på omtrentlig 0,2 prosent inneværende måned.

Endringen i tolvmåneders rentedifferanse er også inkludert i modellen og utgjør over 1/3 av forklaringsgraden. En økning i rentedifferansen på 100 basispunkter gir en appresiering av kronekursen på 2,8 prosent. Dette er i tråd med tidligere empiri for andre estimeringsperioder rapportert av Bernhardsen (2008) og Akram (2019). 

Oljeprisen utgjør også over 1/3 av forklaringsgraden. En økning i oljeprisen på 10 prosent gir en appresiering av kronekursen på om lag 0,6 prosent, noe som er i tråd med Bernhardsen (2008) og Bernhardsen og Røisland (2000), som rapporterer tilsvarende effekter på henholdsvis 0,5 prosent og 0,2 prosent.

Det siste leddet i korttidsmodellen er feiljusteringsleddet, som er innrammet i klammeparentes. Koeffisienten til feiljusteringsleddet gir en indikasjon på hvor lang tid kronekursen bruker på å komme tilbake til nivået som ansees å være likevekt i de tilfellene det har vært avvik (Bernhardsen og Røisland, 2000). Det vil si at i de tilfellene kronekursen er svakere enn det likevektskursen antyder, vil kronen appresiere mot likevekt og avvikene dermed minimeres. Modellen vi har fremstilt reduserer avviket med omtrent 15,5 prosent hver måned, noe som gir en halveringstid¹⁴ på i overkant av 4 måneder.

Ved å gjennomføre ulike diagnostiske tester for modellen, undersøker vi hvor godt spesifisert korttidsmodellen fremstår. Dette gir en indikasjon på påliteligheten og fortolkningen av estimatene ovenfor.

Tabell 4: Diagnostiske tester for korttidsdynamikk

Diagnostiske tester
AR 1-6	F(6,213)	1.25[0.28]
ARCH 1-6	${\chi }^2\left(6\right)$	6.85[0.34]
Normalitetstest	${\chi }^2\left(2\right)$	1.39[0.50]
Skjevhet		0.1739
Kurtose – 3		0.0719
Heteroskedastisitet	F(4,219)	1.55[0.19]
Spesifikasjonstest, RESET	F(3,216)	0.04[0.99]

Tabell 4 viser at vi kan beholde nullhypotesen om ingen autokorrelasjon i residualer opptil 6.orden. Videre kan vi også beholde nullhypotesen om ingen autokorrelasjon i residualvarians opptil 6.orden. Avviket i skjevhet er noe større enn kurtose-3, men residualene fremstår som rimelig normalfordelte ved at testen klart beholder nullhypotesen. Test for heteroskedastisitet viser også at vi kan beholde nullhypotesen om konstant varians. Til slutt viser RESET-testen at vi kan beholde nullhypotesen om ingen utelatte variabler. Tabell 4 viser med andre ord at modellen ikke viser tegn til feilspesifikasjon.

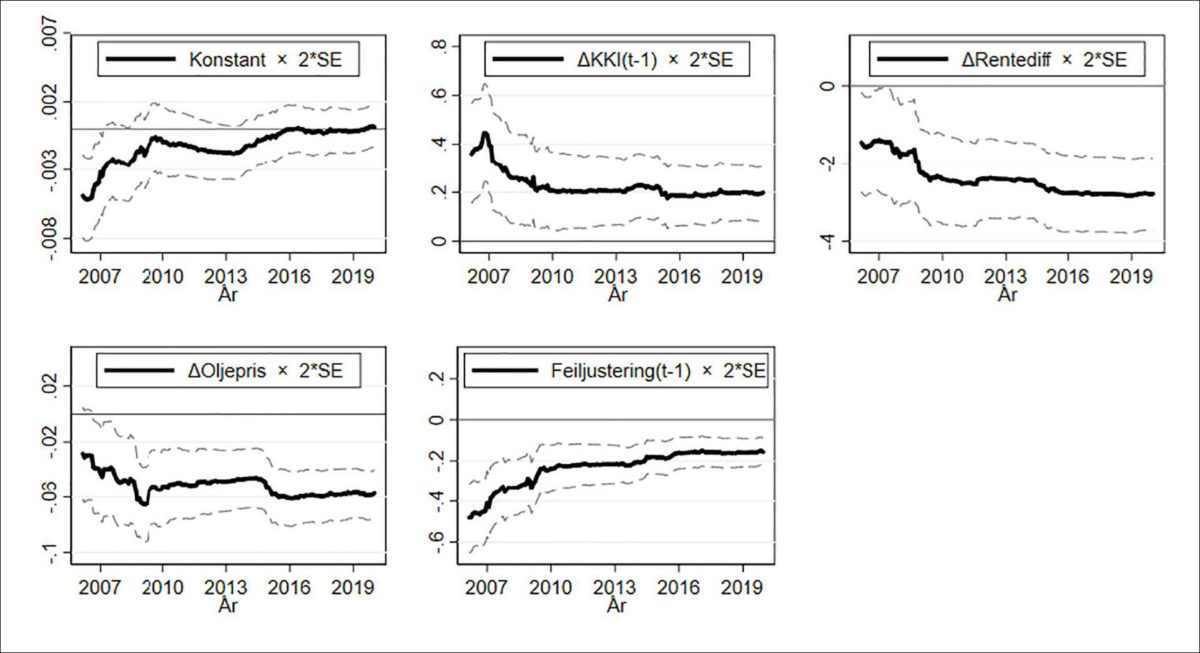
Figur 6 viser at alle koeffisientene virker rimelig stabile ved å plotte rekursive estimater av koeffisientene med en utgangsmodell fra 2001M4 til 2006M3. Det er verdt å merke seg at alle variablene er signifikante for tilnærmet hele rekursjonsperioden.

Konklusjon

Det er en ganske omfattende dokumentasjon av at hverken økonomer eller makroøkonomiske modeller er i stand til å lage prognoser for valutakursen som systematisk og over tid slår dagens kurs. Dette er det enkle prinsippet som følger av at tidsserier for valutakurser har vist seg å oppføre seg tilnærmet som random walk. Det er likevel av verdi å kjenne til hva som er de viktigste driverne av valutakursen for å kunne vurdere om det er faktorer av permanent eller midlertidig karakter som har beveget kursen. For den norske kronen finner vi, i samsvar med tidligere studier, at oljepris, rentedifferanse mot utlandet og indikatorer for internasjonal finansiell ustabilitet påvirker kronekursen. Fallet i oljeprisen i 2015 bidro utvilsomt til å svekke kronen, men den alene ser ikke ut til å forklare den permanente kronesvekkelsen. Oljeprisen har kommet en god del opp fra de laveste nivåene uten at kronen har styrket seg. I vår empiriske valutakursmodell er det den økende forskjellen mellom prisnivå i Norge og hos handelspartnerne som bidrar vesentlig til at estimatet på den langsiktige likevektsverdien av kronen holder seg lavere enn for noen år siden. Med denne biten på plass burde aktørene i valutamarkedet innstille seg på at den norske kronen i gjennomsnitt er omtrent der den skal være.

Fotnoter:

1. Denne artikkelen bygger på materiale fra Myrstuen og Sylte (2020). Takk til redaktør og en anonym konsulent for nyttige kommentarer og innspill til tidligere utkast. ↩︎
2. Ved å betale mer for én enhet utenlandsk valuta, betyr det at NOK blir mindre verdt i forhold til den andre valutaen. Vi bruker begrepene depresiering eller svekkelse av kronen når for eksempel eurokursen øker fra 9 til 10 kroner. ↩︎
3. Den samme sjeføkonomen som bommet med 1 krone i 2018 bommet i samme retning med 1 krone og 5 øre i 2019. ↩︎
4. Se Landberg og Tellesbø (2005), Marthinsen og Rakli (2010), With og Ørjasæter (2017). Neely og Sarno (2002) viser at valutaprognoser basert på makroøkonomiske modeller over tid ikke gjør det systematisk bedre enn random walk, hvor prognoseverdien settes lik kursen i utgangspunktet. ↩︎
5. Dette er en indeks som viser kroneverdien mot Norges 25 viktigste handelspartnere. Høyere verdi betyr svakere kronekurs. ↩︎
6. Bernhardsen (2008), Johansen og Pedersen (2017), Kvam (2017). ↩︎
7. Vektene er valgt med utgangspunkt i vektene for valutakursindeksen KKI, men renter for mindre land er sløyfet. Vektene er de samme som er oppgitt i tabell 1 lengre nede. ↩︎
8. Vektene for utlandet er også her de samme som er oppgitt i tabell 1. ↩︎
9. Det som satte oss på sporet av dette var en kommentar fra Svein ­Gjedrem under en forelesning på NHH. ↩︎
10. Det vil si en tidsserie hvor gjennomsnittet og variansen er konstant, og kovariansen mellom y_t og y_t+h avhenger kun av distansen ​h​, men ikke tidspunktet for når observasjonene er gjort. ↩︎
11. Kurtose og skjevhet er mål på avvik fra symmetrien i en statistisk normalfordeling. Kurtosen sier noe om hvor fete halene til fordelingen er, mens skjevhet indikerer om fordelingen er vridd mot høyre eller venstre. ↩︎
12. Vi har benyttet Johansen-testen for å identifisere om det eksisterer ­kointegrerte forhold mellom tidsseriene (Johansen, 1988). Det vil si om det eksisterer langsiktige likevektsforhold mellom variablene. ↩︎
13. Tester for restriksjoner på både kointegrasjonsvektoren og justeringsparameterne, er basert på Boswijk (1995) og Johansen (1995). ↩︎
14. Formel for halveringstid: (ln(0.5)/(ln(1- θ)), der θ er koeffisienten til feiljusteringsleddet (Bernhardsen & Røisland, 2000). ↩︎