Kapitalverdimodellen: Nøytral skatt på aksjeavkastning og formue
Vi analyserer aksjonærbeskatningen og formuesskatten og ser på nøytralitet mellom avkastning og risiko målt ved Sharpe-raten. Vår studie finner at aksjerabatten på aksjers formuesverdi gir samme tillegg i risikopremien for alle aksjer. Sett i forhold til risikoen fremstår mindre risikable aksjer som mer attraktive. Dermed får investoren incitament til å vri aksjeinvesteringen bort fra mer risikable aksjer og mot mindre risikable aksjer. Samtidig betyr aksjerabatten at aksjer fremstår som mer attraktive relativt til risikofri posisjon, slik at investoren får incitament til å øke aksjeandelen. Aksjerabatten bryter dermed med prinsippet om at skattereglene ikke bør påvirke hvilke investeringer som gjennomføres.
Kapitalverdimodellen: Nøytral skatt på aksjeavkastning og formue1
Innledning
Et viktig bærende prinsipp for skattesystemet i Norge er at skattereglene i minst mulig grad bør påvirke hvilke investeringer som gjennomføres og hvordan en virksomhet organiseres. Dette prinsippet, ofte kalt effektivitetsprinsippet, er ment å sikre at det investeres der hvor avkastning før skatt er høyest fordi det fremmer økonomisk vekst. Bjerksund og Schjelderup (2021a, 2021b, 2022) viser at vi ikke har nøytralitet i hvordan en investor organiserer sine investeringer/sparing. Hovedresultatet i disse arbeidene er at det lønner og investere/spare gjennom en bedrift snarere enn på personlig hånd.
Utgangspunktet for analysen er en investor som sparer på privat hånd. Det økonomiske rammeverket er en liten åpen økonomi hvor kapitalverdimodellen holder. Lånerenten tilsvarer risikofri rente rf. Sharpe -raten måler forholdet mellom avkastning og risiko. Vi ser først på nøytralitet i Sharpe-raten med ett risikabelt aktivum (markedsporteføljen) og risikofri posisjon. Deretter ser vi på et marked med mange aksjer og risikofri posisjon, og etablerer at nøytralitet i Sharpe-raten korresponderer til nøytralitet i sammensetningen av investorens aksjeportefølje. Vi finner at en skjermingsrente som speiler risikofri rente og lik skattlegging av formuesobjekter (altså ingen aksjerabatt) gir nøytralitet. Effekten av aksjerabatten er et tillegg i risikopremien som er det samme for alle aksjer. Det innebærer at sett i forhold til risikoen fremstår lite risikable aksjer som mer attraktive, sammenlignet med mer risikable aksjer. Dermed får investoren incitament til å vri allokeringen av kapital mellom aksjer bort fra mer risikable aksjer og i retning av mindre risikable aksjer. Samtidig betyr aksjerabatten at aksjer fremstår som mer attraktive i forhold til risikofri posisjon, slik at investoren får incitament til å vri allokeringen av kapital bort fra risikofri posisjon og i retning av aksjer. Aksjerabatten bryter dermed med prinsippet om at skattereglene i minst mulig grad bør påvirke hvilke investeringer som gjennomføres.
Vi legger til grunn at aksjeavkastning med fradrag av en skjermingsrente i skattlegges med eierskattesats . Gevinst og tap antas behandlet skattemessig symmetrisk, det vil si at det gis full skatterefusjon for tap. Formuesskatten utlignes på markedsverdi i begynnelsen av perioden og betales i slutten av perioden, med sats for aksjer og sats for andre formuesobjekter. I det norske skattesystemet er satsen for aksjer lavere enn satsen for andre formuesobjekter. Differansen omtales ofte som aksjerabatten i formuesskatten. Vi har særlig fokus på hvordan skjermingsrenten i og aksjerabatten bør fastsettes for å oppnå nøytralitet.2
Vårt arbeid relaterer seg til flere arbeider som ser på investorens formuesskatt eller eierskatt innenfor rammen av kapitalverdimodellen. Sandvik (2016) analyserer formuesskatt på unoterte foretak, og bemerker for noterte foretak at «formuesskatten ikke påvirker verdien av foretaket, som er velkjent.» Hansen og Sandvik (2022) studerer rabatten ved formuesskattegrunnlaget for aksjer, og finner at den øker investorens betalingsvilje for lite risikable aksjer og reduserer betalingsviljen for risikable aksjer, sammenlignet med markedsprisen. Sandvik (2022) ser på den norske aksjonærbeskatningen og finner at den er nøytral med hensyn på sammensetningen av investorens risikable portefølje. Han viser at den dermed også er nøytral med hensyn på investorens betalingsvilje for en aksje eller et prosjekt.
I analysen som følger under, viser vi at det norske skattesystemet påvirker både Sharpe-raten og sammensetningen av en risikabel portefølje. Skattesystemet er med andre ord ikke nøytralt. Imidlertid påvirker ikke skattesystemet verdsettelsen av en aksje eller et prosjekt hvis investoren kan tilpasse seg optimalt. Ut fra dette resultatet finner vi sammenhengen mellom investorens avkastningskrav uten og med eier- og formuesskatt.
Nøytralitet i Sharpe-raten: ett risikabelt aktivum
Kapitalverdimodellen3 forklarer hvordan en aksje eller et prosjekt verdsettes i et velfungerende marked, herunder hva slags risiko investor får kompensasjon for å bære. Et hovedresultat er at forventet avkastning (avkastningskravet) kan forklares som risikofri alternativavkastning pluss en risikokompensasjon for aksjens systematiske risiko i forhold til markedsporteføljen. Et annet hovedresultat er at blant alle mulige risikable porteføljer er det markedsporteføljen som har høyest Sharpe-rate. I dette kapitlet tar vi utgangspunkt i sistnevnte hovedresultat.
I likhet med Hansen og Sandvik (2022) og Sandvik (2022) antar vi en liten åpen økonomi hvor dagens priser på aksjene er gitt. Videre legges det til grunn at alle risikable aktiva er omsatt i markedet og at investoren ikke har andre usikre inntekter. La være fremtidsverdien av en posisjon i markedsporteføljen hvor investeringen er og standardavviket er . Vi definerer som fremtidsverdien av en risikofri posisjon hvor investeringen er normalisert til 1.
I dette kapitlet representerer vi markedsporteføljen med en markedsindeks. Vi ønsker å studere investorens tilpasning uten og med eierskatt og formuesskatt, og legger derfor til grunn at fremtidsverdien av en krone investert risikofritt er
(1)
hvor er risikofri rente og er skattesatsen for alminnelig inntekt.
Sharpe-raten måler forholdet mellom risikopremie og risiko for en risikabel investering. Sharpe-raten til markedsporteføljen på verdiform gis ved4
(2)
hvor risikopremien i telleren er definert ved differansen mellom forventningen ( og den sikre fremtidsverdien( ), dvs. . I nevneren finner vi investeringens risiko målt ved standardavviket. Sharpe-raten gir oss dermed investeringens risikopremie per enhet risiko.
Vi ser nå på fremtidsverdier med eierskatt og formuesskatt av en krone investert. I vår analyse antar vi at formuesskatten utlignes på markedsverdi i begynnelsen av perioden og betales i slutten av perioden.5
Investorens fremtidsverdi av en krone investert risikofritt (for eksempel bankkonto eller et sikkert rentepapir) med disse skattene er
(3)
hvor er fremtidsverdien uten disse skattene gitt ved ligning (1) og er satsen for annen formue enn aksjer. Merk at det ikke er eierskatt på denne investeringen.
Den usikre fremtidsverden av en krone investert i markedsporteføljen med eier- og formuesskatt blir
(4)
hvor er fremtidsverdien uten skatt, er sats for eierskatt, i er skjermingsrenten og er sats for aksjeformue. Merk at siden normalavkastningen gitt ved skjermingsrenten skal skjermes fra beskatning i det norske skattesystemet kommer leddet til fratrekk fra fremtidsverdien når eierskatten skal beregnes, se uttrykket mellom de to likhetstegnene i ligning (4). Det følger fra ligning (4) at forventet fremtidsverdi med eier- og formuesskatt blir
(5)
hvor er forventet fremtidsverdi uten disse skattene. Risikopremien med eier- og formuesskatt blir
(6)
hvor er risikopremien uten disse skattene og hvor er definert ved
(7)
Risikoen (standardavviket) til fremtidsverdien med eier- og formuesskatt blir
(8)
hvor er standardavviket til fremtidsverdien uten disse skattene. Sharpe-raten til investeringen i markedsporteføljen med eierskatt og formuesskatt blir dermed
(9)
hvor vi setter inn for ligning (6) og (8) og bruker ligning (2). Det følger fra ligning (9) at Sharpe-raten til investeringen i markedsporteføljen med eierskatt og formuesskatt er lik Sharpe-raten til markedsporteføljen uten disse skattene hvis ξ=0,dvs.
(10)
Vi kan fortolke som et mål på skatteforstyrrelsen, det vil si i hvilken grad eier- og formuesskatten samlet sett avviker fra nøytralitet.
Fra definisjonen av i ligning (7) ser vi at hvis hvert av de to leddene på høyre side er lik null oppnås nøytralitet. Fra ligning (1) vet vi at fremtidsverdien av den risikofrie investeringen er Vi kan dermed utlede følgende nøytralitetsresultat fra ligning (9):
(11)
Vi har dermed vist at med dagens skjermingsrente i eierskatten (jf. aksjonærmodellen) og ingen aksjerabatt i formuesskatten, er Sharpe-raten for markedsporteføljen med og uten disse skattene den samme.
Videre følger det fra ligningene (7) og (9) at med dagens skjermingsrente og aksjerabatten slik den er innført i det norske skattesystemet, at
(12)
Dermed kan vi konkludere med at aksjerabatten bryter med nøytralitetskriteriet om at Sharpe-raten ikke skal påvirkes av skattene.
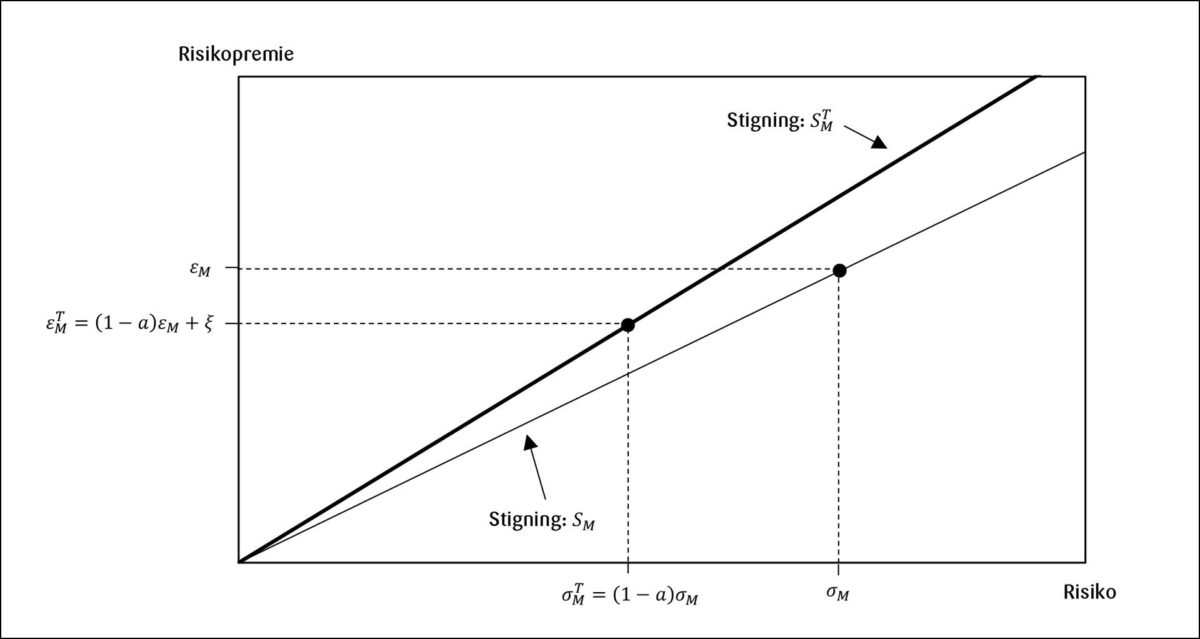
Figur 1 illustrerer markedsporteføljens Sharpe-rate med og uten eier- og formuesskatt med skatteforstyrrelse. Risiko og risikopremie etter disse skattene er gitt ved ligningene (6) og (8). Den rette linjen som går fra origo er kapitalallokeringslinjen, altså investorens meny når markedsporteføljen blandes med risikofri posisjon. Sharpe-raten tilsvarer helningen på kapitalallokeringslinjen. Vi ser av Figur 1 at skatteforstyrrelsen medfører at stigningen til den fete kapitalallokeringslinjen( ) er større enn stigningen til den andre ( ).
Nøytralitet i Sharpe-raten: flere risikable aktiva
I dette kapitlet betrakter vi situasjonen hvor markedsporteføljen er satt sammen av flere risikable aktiva. Vi er innenfor et rammeverk hvor investering i aksjer er beskrevet ved forventing, varians og kovarians og hvor det er et risikofritt aktivum. Innenfor dette rammeverket er det optimalt for investoren å sette sammen aksjeporteføljen slik at Sharpe-raten blir størst mulig. Forklaringen på dette er at investoren dermed skaffer seg den beste menyen å velge fra når investoren, gitt sin holdning til risiko, i neste omgang skal fordele sin formue mellom den optimale aksjeporteføljen og risikofri posisjon. Det følger av dette at investorer som oppfatter markedet likt vil ha samme sammensetning av aksjeporteføljen, selv om de har ulik holdning til risiko.6
Nøytralitetsresultatet i ligning (11) sier at Sharpe-raten til investeringen i markedsporteføljen ikke påvirkes av skattene med en skjermingsrente lik dagens og hvis alle formuesobjekter skattlegges med samme sats. I det følgende skal vi vise et utvidet nøytralitetsresultat, nemlig at med skjermingsrente lik dagens og ingen aksjerabatt blir sammensetningen av aksjeporteføljen også den samme med og uten eier- og formuesskatt.
For å vise dette resultatet skal vi anta at markedet består av aksjer. I det følgende benyttes matrisenotasjon, slik at alle vektorer har dimensjon og matriser har dimensjon . Dagens pris på aksjene er hvor element er prisen på aksje . De fremtidige usikre aksjeprisene er gitt ved , hvor element er fremtidig pris for aksje med forventning . Risikopremien til aksjene er gitt ved 𝛆 hvor element er risikopremien til aksje . Usikkerheten er beskrevet ved varians- kovariansmatrisen hvor hvert element er gitt ved . Vi forutsetter at økonomien er uten risikofrie arbitrasjemuligheter og at det ikke er mulig å kopiere den fremtidige usikre prisen til noen av aksjene ved å holde en kombinasjon av andre aksjer. 7
Sammensetningen av markedsporteføljen er gitt ved vektoren , hvor element er vekten for aksje . Samlet investering utgjør , hvor er den transponerte til . Det betyr at , altså produktet av vekten for aksje og aksjens pris, er andelen av markedsporteføljen som er investert i denne aksjen.
Risikopremien til markedsporteføljen er
(13)
mens standardavviket er
(14)
Ved å sette ligningene (13) og (14) inn i ligning (2) kan vi uttrykke Sharpe-raten til markedsporteføljen uten eier- og formuesskatt slik
(15)
hvor er vektene som maksimerer gitt at budsjettbetingelsen
(16)
holder. Med andre ord, gitt beskrivelsen av markedets avkastningsmuligheter gir markedsporteføljen høyest Sharpe-rate før skatt.8
Vi vil nå ta inn eier- og formuesskatt i analysen. Fremtidsverdien av en krone investert risikofritt med eier- og formuesskatt er gitt ved ligning (3) ovenfor. Den usikre fremtidsverdien av en krone investert i aksje j med eier- og formuesskatt kan uttrykkes slik
(17)
hvor er fremtidsverdien av en krone investert i aksjen uten skatt, er sats for eierskatt, er dagens pris, er skjermingsrente og er sats for aksjeformue.
Det følger fra ligning (17) at forventet fremtidsverdi for aksje j med eier- og formuesskatt blir
(18)
hvor .
Risikopremien for aksje j med eier- og formuesskatt blir
(19)
hvor er risikopremien uten disse skattene, og hvor er definert i ligning (7). Kovariansen mellom de fremtidige prisene til aksje og med eierskatt og formuesskatt blir
(20)
Vi lar nå være aksjenes risikopremie med eier- og formuesskatt hvor element er gitt ved ligning (19), og kovariansmatrisen hvor element er gitt ved ligning (20). Sammenhengen mellom aksjenes risikopremie og risiko med og uten eier- og formuesskatt er dermed gitt ved
(21)
(22)
La nå vektoren v være en vilkårlig sammensetning av den risikable porteføljen med eier- og formuesskatt hvor element vj er vekten for aksje j. Risikopremien til denne porteføljen er
(23)
mens standardavviket er
(24)
Ved å sette ligningene (23) og (24) inn i ligning (2) kan vi uttrykke Sharpe-raten til denne porteføljen med eier- og formuesskatt slik
(25)
gitt at budsjettbetingelsen
(26)
holder.
La oss se på Sharpe-raten til markedsporteføljen med eier- og formuesskatt. Ved å sette v=m inn i ligning (25) og utnytte ligning (8) får vi
(27)
Første ledd er markedsporteføljens Sharpe-rate uten disse skattene, se ligning (15), ξ er skatteforstyrrelsen gitt ved ligning (7), og σM i nevneren til det siste leddet er gitt ved ligning (14).
De optimale vektene med eier- og formuesskatt, w, er gitt ved
Tangentporteføljen bestemmes fra hvor er en konstant og er porteføljevektene. Det følger fra dette at
(28)
hvor vi i ligning (28) maksimerer med hensyn på vektene .
Fra ligning (27) og (28) følger det at
(29)
Det vil si at uten skatteforstyrrelsen blir både investorens Sharpe-rate og den optimale sammensetning av den risikable porteføljen med eier- og formuesskatt tilsvarende som for markedsporteføljen.
Figur 2 illustrerer situasjonen uten skatteforstyrrelse. Uten skatteforstyrrelsen blir porteføljefronten (den krumme stiplede kurven i Figur 2) trukket nærmere origo som følge av at eierskatten skalerer ned både risikopremien og risikoen. Dermed vil helningen til porteføljesammensetningen være den samme med og uten eier- og formueskatt, dvs. .
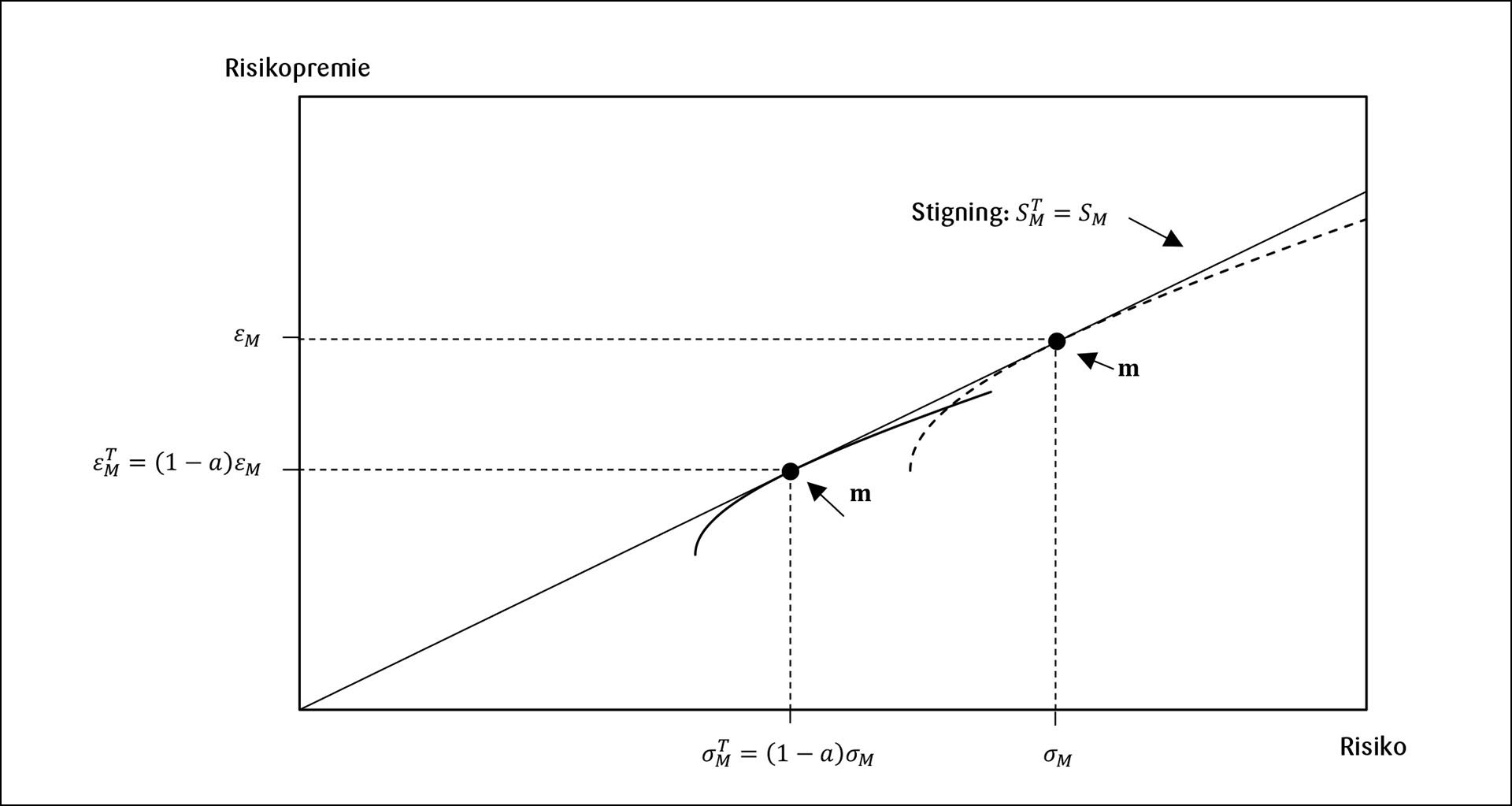
Figur 2:
Porteføljesammensetning m uten skatteforstyrrelse 𝜉=0.
Sandvik (2022) ser bort fra formuesskatten og studerer aksjonærbeskatningen innenfor rammen av kapitalverdimodellen. Han viser at med dagens skjermingsrente er investorens optimale sammensetning av den risikable porteføljen den samme med og uten eierskatt. Vi har ovenfor sett at skjermingsrente og samme formuesskattesatser leder til og nøytralitet. Vårt resultat i ligning (29) er derfor konsistent med Sandviks resultat.
La oss nå anta en skatteforstyrrelse Det følger da fra ligning (27) og (28) at
(30)
Det vil si at med eier- og formuesskatt blir investorens Sharpe-rate høyere enn raten for markedsporteføljen. Videre blir den optimale porteføljesammensetningen forskjellig fra markedsporteføljens sammensetning. I det følgende skal vi se nærmere på hva skatteforstyrrelsen betyr for investorens aksjeportefølje.
Hansen og Sandvik (2022) ser bort fra eierskatt og studerer formuesskatt med aksjerabatt innenfor rammen av kapitalverdimodellen. De finner at investorens verdsettelse av aksjer påvirkes av aksjonærrabatten i formuesskatten ved at lite risikable aksjer (beta mindre enn 1) verdsettes høyere med formuesskatt enn uten, og at mer risikable aksjer (beta større enn 1) verdsettes lavere. Resultatet i Hansen og Sandvik (2022) er basert på en antakelse om at investoren holder markedsporteføljen uten og med skatt, det vil si at porteføljesammensetningen er m i begge tilfeller.
I vedlegget viser vi at når investoren holder porteføljesammensetningen m blir investorens betalingsvilje for en aksje med eier- og formuesskatt, , lik
(31)
hvor er aksjens beta uten disse skattene. Med antakelsene til Hansen og Sandvik, det vil si ingen eierskatt og aksjerabatt i formuesskatten, har vi positiv skatteforstyrrelse og deres resultat følger umiddelbart. Vi får tilsvarende resultat hvis vi antar skjermingsrente og aksjerabatt i formuesskatten, eller hvis vi antar at skjermingsrenten og ingen aksjerabatt i formuesskatten.
Hvis investoren kan tilpasse seg optimalt med eier- og formuesskatt, vil investoren ha incitament til vekte seg opp i lite risikable aksjer (beta mindre enn 1) og vekte seg ned i risikable aksjer (beta større enn 1). Dette vil skje inntil investoren oppnår den optimale porteføljesammensetningen w hvor betalingsviljen for hver enkelt aksje tilsvarer aksjens markedspris.
Når investoren endrer sin portefølje som beskrevet ovenfor, blir betaen for den risikable porteføljen lavere enn den for markedet, det vil si at . Det betyr at forventet avkastning for denne porteføljen blir lavere enn forventet avkastning for markedsporteføljen.
La oss nå se på hva som skjer med totalrisikoen. Ovenfor har vi funnet at porteføljen W har høyere Sharpe-rate enn markedsporteføljen, det vil si . Husk at Sharpe-raten er forholdstallet mellom risikopremie og totalrisiko (standardavviket). Vi kan skrive dette som
(32)
hvor vi forklarer risikopremien til portefølje W ved hjelp av betaen. Det følger umiddelbart fra ligning (32) at
(33)
Når investoren kan tilpasse seg optimalt blir resultatet av skatteforstyrrelsen at investoren holder en mindre risikabel aksjeportefølje enn markedsporteføljen.
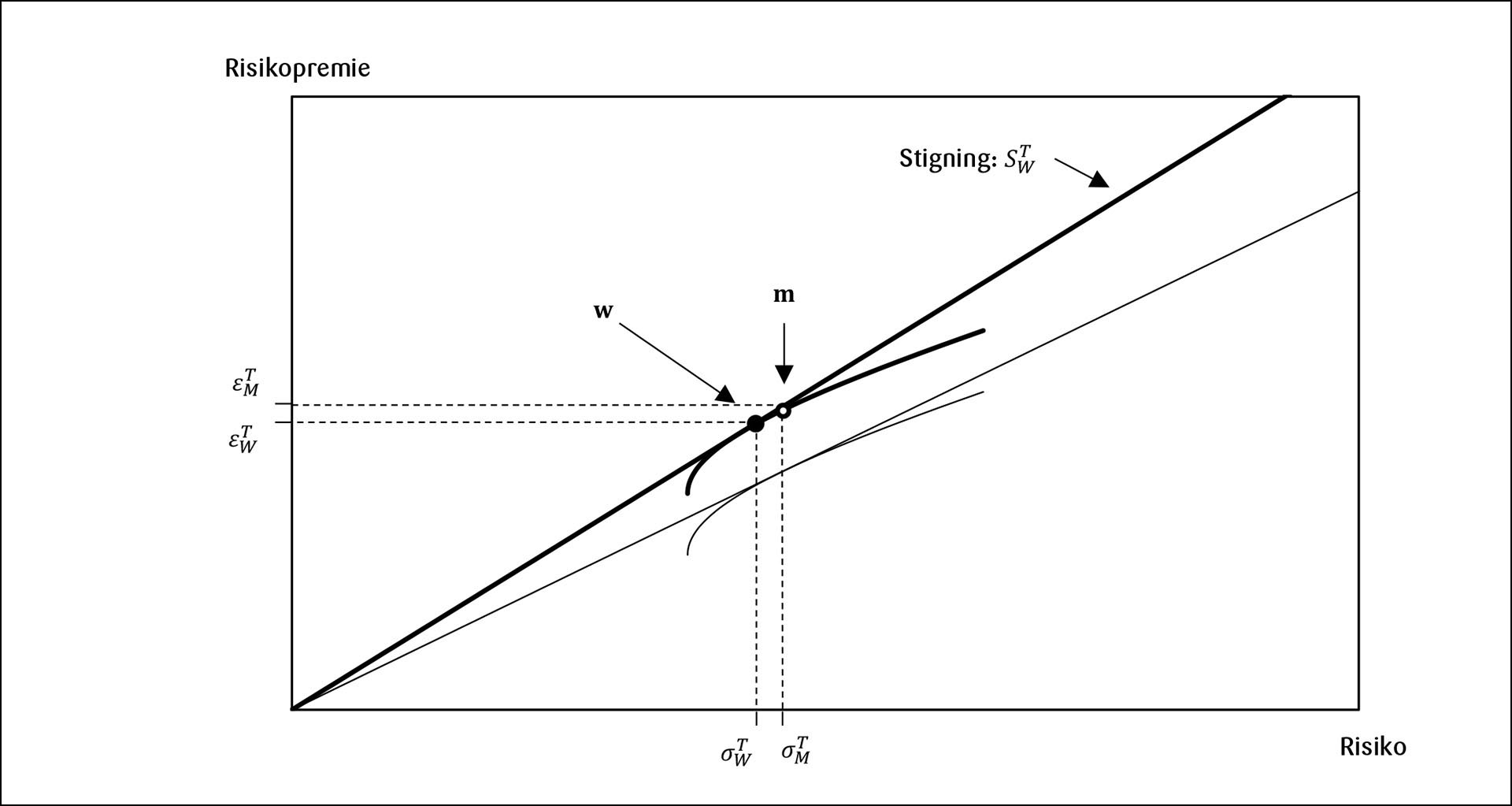
Figur 3:
Porteføljesammensetning w med skatteforstyrrelse 𝜉>0.
La oss se nærmere på tilfellet med positiv skatteforstyrrelse, jf. Figur 3. En positiv skatteforstyrrelse medfører samme tillegg i risikopremien for alle aksjer slik at porteføljefronten skifter oppover i diagrammet, mens helningen i hvert punkt på porteføljefronten er den samme. Anta en investor som i utgangspunktet har porteføljesammensetning m. Dette betyr at for porteføljesammensetningen mblir helningen til porteføljefronten mindre enn Sharpe-raten. Investoren kan da oppnå en høyere Sharpe-rate ved å bevege seg nedover langs porteføljefronten. Siden porteføljefronten krummer nedover, er den optimale porteføljesammensetningen wgitt ved punktet på porteføljefronten hvor helningen er lik Sharpe-raten t til dette punktet. Vi har dermed at med en positiv skatteforstyrrelse er Sharpe-raten til porteføljen W høyere enn den for markedsporteføljen M. Videre ser vi av figuren at porteføljen W har både lavere risikopremie og lavere totalrisiko enn markedsporteføljen M, dvs. og .
Aksjerabatten medfører et tillegg i risikopremien som er det samme for alle aksjer uansett risiko. Når dette tillegget i risikopremien sees i forhold til aksjens risiko, vil lite risikable aksjer fremstå som mer attraktive sammenlignet med mer risikable aksjer. Dette har som konsekvens at investorens allokering av kapital mellom aksjer vris bort fra mer risikable aksjer og i retning av mindre risikable aksjer. Aksjerabatten bryter dermed med prinsippet om at skattereglene i minst mulig grad bør påvirke hvilke investeringer som gjennomføres.
Allokering mellom aksjeporteføljen og risikofri posisjon
Ovenfor har vi sett på sammensetningen av aksjeporteføljen. Utgangspunktet er at aksjeporteføljen settes sammen slik at Sharpe-raten blir høyest mulig. Investorer som oppfatter markedet likt, vil holde den samme aksjeporteføljen selv om de har ulik grad av risikoaversjon.
Investorens risikoaversjon vil imidlertid ha betydning for hvordan formuen fordeles mellom aksjer og risikofri posisjon. Vi ønsker å se effekten av aksjerabatten på investorens kapitalallokering med eier- og formuesskatt. La være fremtidsverdien etter skatt av en krone investert i aksjeporteføljen og være fremtidsverdien etter skatt av en risikofri posisjon på en krone. La være andelen av formuen som plasseres i aksjer og risikofri posisjon. Fremtidsverdien av en slik plassering, , kan kan uttrykkes ved
(34)
Vi antar nå at investoren har preferanse definert over forventning og varians gitt ved
(35)
hvor A>0 er koeffisienten for relativ risikoaversjon. Investorens optimale aksjeandel er gitt ved
(36)
hvor vi bruker definisjonen av risikopremie og Sharpe-rate. Merk at aksjeandelen er bestemt ved aksjeporteføljens Sharpe-rate og risiko, samt risikoaversjonsparameteren.9
(37)
hvor er markedsporteføljens Sharpe-rate og er markedsporteføljens risiko etter skatter. Med en positiv skatteforstyrrelse holder investoren aksjeporteføljen W med sammensetningen w, slik at den optimale aksjeandelen blir
(38)
hvor er Sharpe-raten og er risikoen til portefølje etter skatter.
Fra ligning (30) og (33) fant vi at med en positiv skatteforstyrrelse har porteføljen høyere Sharpe- rate og lavere risiko . Det følger umiddelbart fra ligning (37) og (38) at
(39)
det vil si at en positiv skatteforstyrrelse (aksjerabatten) medfører at aksjeandelen blir høyere.
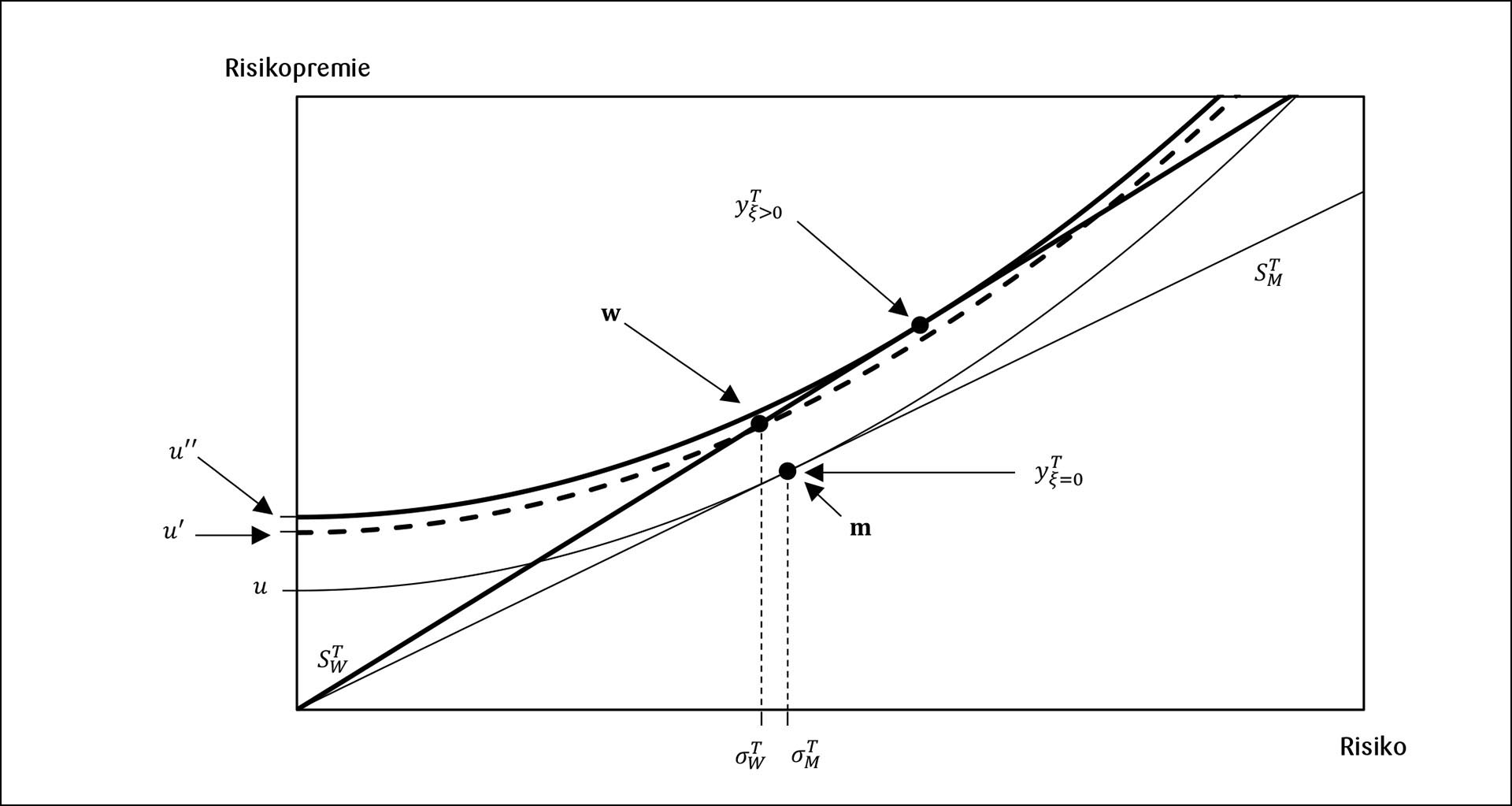
Denne effekten er illustrert i Figur 4. Kurvene som krummer oppover er indifferenskurver, det vil si kombinasjoner av risikopremie og risiko som investoren anser som likeverdige. Merk at den vertikale avstanden mellom hvert par av kurver er uavhengig av risiko, slik at for en gitt risiko er helningen til indifferenskurvene den samme. Investoren ønsker en tilpasning lengst mulig opp og til venstre i figuren.
Figur 4:
Aksjeandel
uten og med skatteforstyrrelse.
Uten skatteforstyrrelse tilpasser investoren seg på den nederste kapitalallokeringslinjen, det vil si den som har stigning . For å forenkle figuren har vi antatt at investorens preferanse er slik at den optimale aksjeandelen er 1, det vil si at hele formuen investeres i markedsporteføljen. Dette betyr at den nederste indifferenskurven tangerer den nederste kapitalallokeringslinjen i punktet som svarer til markedsporteføljen angitt ved aksjesammensetningen m.
Med positiv skatteforstyrrelse tilpasser investoren seg på den øverste fete kapitalallokeringslinjen, det vil si den som har stigning . Dette tilsvarer investorens meny med den optimale aksjeporteføljen , som er angitt med aksjesammensetningen . Den midterste indifferenskurven skjærer gjennom kapitalallokeringslinjen i punktet som svarer til den optimale aksjeporteføljen , og speiler investorens nytte av å velge en aksjeandel på 1. Merk at helningen til indifferenskurven i dette punktet er mindre enn helningen på kapitalallokeringslinjen. Det betyr at investoren kan komme bedre ut ved å velge en høyere aksjeandel, som i dette tilfellet vil si lånefinansiering. Investorens optimale tilpasning er punktet angitt ved hvor den øverste indifferenskurven tangerer kapitalallokeringslinjen.
Aksjerabatten betyr at den optimale aksjeporteføljen fremstår som mer attraktiv sammenlignet med risikofri posisjon. Det har som konsekvens at investorens allokering av kapital mellom aksjer og risikofri posisjon vris i bort fra risikofri posisjon og i retning av aksjer. Aksjerabatten bryter dermed med prinsippet om at skattereglene i minst mulig grad bør påvirke hvilke investeringer som gjennomføres.
Forventet avkastning og avkastningskrav
Et utgangspunkt for vår analyse er en liten åpen økonomi hvor aksjeprisene er gitt og hvor investoren er pristaker. Det innebærer at for investoren er forventet avkastning for aksje j uten skatter
(40)
Forventet avkastning for aksje j med skatter kan skrives som 10
(41)
Normalt vil begge de to siste leddene på høyresiden være negative, slik at skattene medfører lavere forventet avkastning for investoren.
Vi kan forklare investorens verdsetting av aksje uten skatter slik
(42)
hvor er kapitalavkastningskravet uten eier- og formuesskatt. Vi har antar at investoren er optimalt tilpasset (porteføljevekter m) og da følger det fra optimalitet at investorens betalingsvilje for aksje er lik aksjens pris.
La oss dernest se på situasjonen med eier- og formuesskatt. Vi antar at investoren er optimalt tilpasset (porteføljevekter w) slik at det følger fra optimalitet11 at investorens betalingsvilje for aksje j er lik aksjens pris. Dermed kan vi uttrykke investorens betalingsvilje for aksjen, dvs. slik
(43)
hvor er kapitalavkastningskravet med eier- og formuesskatt.
Dette leder til at vi kan uttrykke kapitalavkastningskravet med skatter, ,slik
(44)
hvor er kapitalavkastningskravet uten skatter fra ligning (42). Normalt vil begge de to siste leddene i ligning (44) være negative, slik at skattene medfører at investorens avkastningskrav med skatt er lavere enn uten.
Gitt at investoren er optimalt tilpasset er investorens betalingsvilje for aksje j den samme med og uten skatter. Forklaringen på dette er at investorens forventede avkastning er lavere med skatter enn uten, samtidig som investorens kapitalavkastningskrav også er lavere, og at de to effektene utligner hverandre når investoren er optimalt tilpasset. Dette er konsistent med resultatene i Bjerksund og Schjelderup (2021c) som analyserer investorens verdsettelse av et prosjekt.
Oppsummering
Aksjonærmodellen medfører at utbytte ut over et skjermingsfradrag skattlegges på personlig aksjonærs hånd med eierskatten. Skjermingsfradraget fastsettes av skjermingsrenten. Vi har vist at hvis skjermingsrenten settes slik den er fastsatt i dag i det norske skattesystemet og alle formuesobjekter skattlegges med samme sats, påvirker skattesystemet verken Sharpe-raten eller investors sammensetning av en risikabel portefølje.
Solberg-regjeringens innføring av aksjerabatt medfører lavere formuesskatt på aksjer. Effekten av aksjerabatten er et tillegg i risikopremien som er likt for alle aksjer. Det innebærer at sett i forhold til risikoen fremstår lite risikable aksjer som mer attraktive, sammenlignet med mer risikable aksjer. Dermed får investoren incitament til å vri allokeringen av kapital mellom aksjer bort fra mer risikable aksjer og i retning av mindre risikable aksjer. Samtidig betyr aksjerabatten at aksjer fremstår som mer attraktive i forhold til risikofri posisjon, slik at investoren får incitament til å vri allokeringen av kapital bort fra risikofri posisjon og i retning av aksjer. Aksjerabatten bryter dermed med prinsippet om at skattereglene i minst mulig grad bør påvirke hvilke investeringer som gjennomføres.
Referanser
Bjerksund, P. og G. Schjelderup (2021a). Aksjonærmodellen og fritaksmetoden: Et to-hodet troll? Samfunnsøkonomen 135 (4), 53–63.
Bjerksund, P. og G. Schjelderup (2021b). Er den norske aksjonærbeskatningen nøytral? Samfunnsøkonomen 135 (4), 43–52.
Bjerksund, P. og G. Schjelderup (2021c). Investor asset valuation under a wealth tax and a capital income tax. International Tax and Public Finance. https://doi.org/10.1007/s10797-021-09691-0
Bjerksund, P. og G. Schjelderup (2022). Investors utbyttebeslutning og formuesskatt. Samfunnsøkonomen 136 (2), 27–34.
Bodie, Z., A. Kane og A. J. Marcus (2021). Investments, 12. utgave. International Student Edition, McGraw-Hill.
Copeland, T. E., J. F. Weston og K. Shastri (2014). Financial Theory and Corporate Policy. Pearson.
Elton, E. J., M. J. Gruber, S. J. Brown og W. N. Goetzmann (2014). Modern Portfolio Theory and Investment Analysis. Wiley.
Hansen, E. og B. Sandvik (2022). Formueskatt med redusert skattegrunnlag for aksjer. Samfunnsøkonomen 136 (1), 40–43.
Sandvik, B. (2016). Formueskatt på noterte foretak. Samfunnsøkonomen 130 (3), 4–7.
Sandvik, B. (2022). Nøytralitet av den norske utbytteskatten. Samfunnsøkonomen 136 (2), 35–38.
Vedlegg 1: Formuesskatten utlignet på verdi i slutten av perioden
Anta nå et skattesystem hvor formuesskatten utlignes på markedsverdien i slutten av perioden. Investorens fremtidsverdi av en krone investert risikofritt blir da
(45)
hvor er satsen for alminnelig personinntekt og er satsen for annen formue enn aksjer. La nå og . Vi har da at , se ligning (3) og ligning (1).
Den usikre fremtidsverdien av en krone investert i markedsporteføljen med eier- og formuesskatt blir
(46)
hvor er satsen for eierskatt, er skjermingsrenten og er sats for aksjeformue. La nå , og . Vi har da at , se ligning (4). Vi har dermed vist at et skattesystem hvor formuesskatten utlignes på markedsverdien i slutten av perioden er ekvivalent med vår modell og analyse.
Vedlegg 2: Verdsettelse av en aksje gitt at markedsporteføljen holdes
I dette vedlegget utledes ligning (31). Kapitalverdimodellen på sikkerhetsekvivalentform12 forklarer markedsprisen på en aksje j slik
(47)
Første ledd i telleren i ligning (47) er forventet fremtidig pris på aksjen. Andre ledd er aksjens risikopremie, som kan skrives som aksjens beta multiplisert med risikopremien for markedsporteføljen. Telleren kan forstås som en sikkerhetsekvivalent verdi, det vil si en sikker fremtidig betaling som anses som like verdifull som den fremtidige usikre prisen til aksje j. Siden risiko er justert for i telleren, speiler diskonteringen i nevneren risikofri avkastning. Aksjens beta og risikopremien til markedsporteføljen, som inngår i telleren i ligning (47), kan uttrykkes som
(48)
(49)
La oss dernest se på investorens betalingsvilje for en aksje j med skatter, gitt at investoren holder markedsporteføljen m. Det følger fra ligning (4) og ligning (17) og regneregler for varians og kovarians at aksjens beta etter skatter blir
(50)
som altså er den samme som uten skatter. Fra ligning (7) har vi at markedsporteføljens risikopremie etter skatter er gitt ved
(51)
hvor vi ser at skatteforstyrrelsen inngår.
Vi finner investorens betalingsvilje med skatter slik. Sett først inn for (5), (6) og (3).
Omgrupperer leddene
hvor vi bruker ligning (47).
Ved å utnytte definisjonen av skatteforstyrrelsen i ligning (7) kan telleren i det første leddet forenkles. Siden er fremtidsverdien av å investere en krone i aksjen, må aksjens markedspris tilsvare . Ved å sette dette inn i telleren det siste leddet, får vi resultatet i ligning (31) ovenfor.
Fotnoter:
- Takk til anonym konsulent og redaktør Lars-Erik Borge for nyttige kommentarer. ↩︎
- Utgangspunktet for beregningen av skjermingsrenten er aritmetisk gjennomsnittlig observert rente på statskasseveksler med 3 måneders løpetid, slik den er rapportert av Norges Bank. Den publiserte renten skal tillegges 0,5 prosentenheter for å fastsette beregningsgrunnlaget. Beregningsgrunnlaget nedjusteres med satsen for alminnelig inntekt, 22 prosent, og avrundes til nærmeste tiendedels prosentpoeng. ↩︎
- Se for eksempel Bodie mfl. (2021), Copeland mfl. (2014) og Elton mfl. (2014). ↩︎
- Her er det en formel ↩︎
- I det norske skattesystemet betaler skattyter formuesskatt av formuen ved årets slutt. I vedlegg 1 viser vi at en modell hvor formuesskatten betales av markedsverdi i slutten av året er ekvivalent med vår modell og analyse, gitt en passende omfortolkning av skatteparametre. ↩︎
- Se for eksempel Bodie mfl. (2021), Copeland mfl. (2014) og Elton mfl. (2014). ↩︎
- Rare tegn/formler ↩︎
- Her skal det være en formel ↩︎
- Se for eksempel Bodie mfl. (2021), Copeland mfl. (2014) og Elton mfl. (2014). ↩︎
- Her skal det være formel ↩︎
- Vi forutsetter her at det ikke er hjørneløsning for denne aksjen. ↩︎
- Se Copeland mfl. (2014) og Sandvik (2016, 2022). ↩︎

