Krona – beveger den seg som en full mann?¹

Introduksjon

Artikkelen studerer den nominelle verdi av den norske krone mot euro. Figur 1 viser utviklingen av kronekursen i perioden 2001–2021. Kursen svinger fra den høyeste notering på over 11 norske kroner (rundt 2020), til den laveste på vel 7 kroner i (2002, 2005 og 2012). Figuren viser brå endringer i kursen tilsynelatende uten sammenheng med tidligere noteringer. Dette bidrar til at det blir vanskelig å spå kronekursens videre utvikling. Klovland, Myrstuen og Sylte (2021) gir eksempler på hvordan norske økonomer i sine spådommer har bommet grovt.

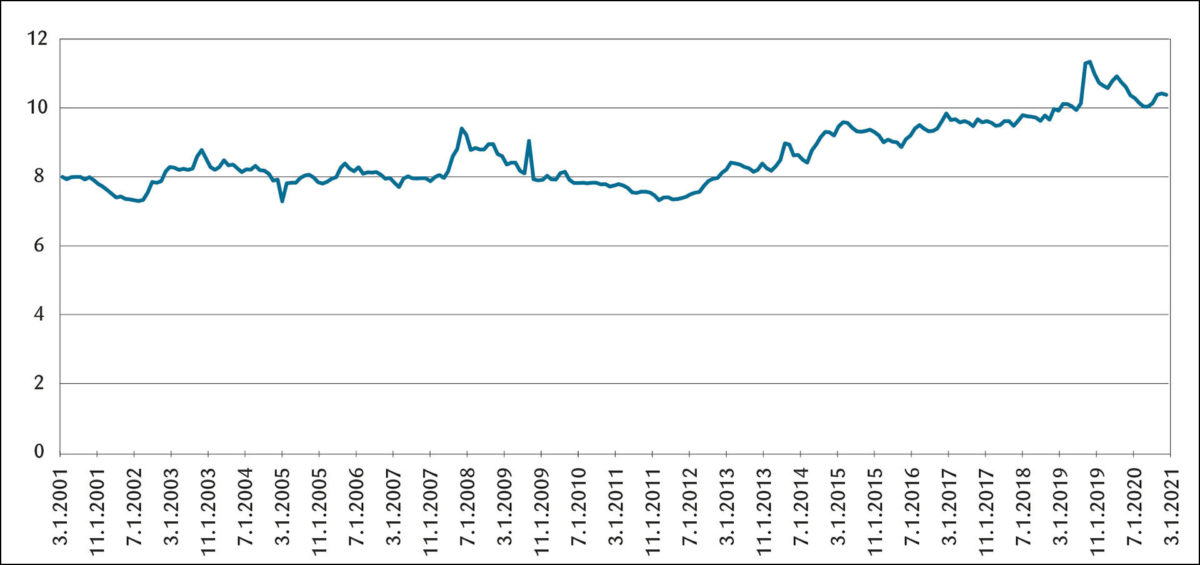
Det er ikke bare norske økonomer som har problemer med å spå valutakurser. Meese-Rogoff (1983) hevder generelt at analyser av valutaer ikke bare gir usikre resultater, disse modellene konkurrerer ikke engang med prognoser som sier at valutakursn utvikler seg helt tilfeldig. Denne klare utfordring for økonomiske modeller, Meese-Rogoff Puzzle, gjelder fortsatt i dag, mener Moosa og Burns (2015). 

Hvorfor er det så vanskelig å spå valutakurser?

Det første svaret på spørsmålet er at valutakursen påvirkes av mange faktorer; økonomiske (priser, renter), markedsmessige forhold ellers samt handelspolitikk i et komplisert samspill (de fundamentale forhold). Det andre svaret er at hvis folk likvel tror at det er enkelt å spå valutakurser og lett å tjene penger i valutamarkedet, vil det komme mange spekulanter til markedet utrustet med innsikt fra markedspsykologi, krydret med hjemmesnekrede markedskunnskaper, og med flokkatferd som vil gitt hopp opp og ned i kursen langt utover hva de fundamentale forholdene skulle tilsi. 

I dette tilfelle vil resultatet bli: Valutakursprognoser som, selv om de skulle inkludere valutaspekulasjon, vil ha problemer med å spå valutakursen, Ja, det er lett å forstå, men at en modell basert på økonomisk teori heller ikke i dag skulle spå bedre enn å kaste mynt, vil være overraskende. 

Formålet med studien 

Er det da en myte at Meese-Rigiff Puzzle fortsatt er aktuell. Dette er et av hovedspørsmålene studien skal se nærmere på.

Analysen gjør bruk av en økonomisk feilkorreksjonsmodell. Det er en modell som brukes til å studere tidsserier når de underliggende variablene har en langsiktig felles stokastisk trend. Begrepet feilkorrigering refererer seg til at når siste observasjon avviker fra langsiktig likevekt, skapes det en dynamikk i modellen gjennom to valutakurser; en på kort sikt og en annen langsiktig likevektskurs. Fokuset i studien skal mest være likevektskursen.

Det er blant annet likevektsløsningen vi vil legge til grunn nå vi skal sammenlikne den økonomiske modellen og RW-modellen når det gjelder å predikere kronekursene framover. Kortidssvingninger har sin verdi på veien til likevektskursen. Jo, mindre avvik det er mellom de predikerte langtidsløsningene og de observerte valutakurser, desto bedre tror vi modellen er.

Som et resultat av økonomisk teori / våre empiriske resultater vil vi få informasjon som er nyttig i andre sammenhenger enn det som er nevnt ovenfor. Det siste året har høy inflasjon igjen vært en verkebyll for verdensøkonomien, de nasjonale økonomier og for folks velferd. Mye av denne prisstigningen er en konsekvens av krigen mellom Russland og Ukraina som har gitt sterkt stigende priser på verdensmarkedet blant annet på energi og matvarer. Norges Bank har et samfunnsoppdrag om å bidra til at vi har en lav prisstigning (2 pst.). Norges Bank kan ikke gjøre noe med prisen på verdensmarkedet. Derimot kan banken ved å endre renten gjøre krona sterkere, som kan redusere prisen i Norge på importvarene. Det siste året har hovedbudskapet til Norges Bank vært at renten må opp for at inflasjonen skal ned. Men når prisstigningen kommer gjennom importpriser er poenget med høyere rente at kronekursen skal styrke seg. Da viser teori / våre empiriske analyser at det er ikke nok at renta går opp i Norge, den må også gå mer opp enn i EU-området og i andre land. 

Arbeidet er organisert i følgende temaer: Økonomiske hypoteser om valutkursen. Spesifisering av en økonomisk modellen, samt en konkurrerende modell (RW-modell). Test av modellene, supplert med beregning av krone kursprediksjoner. Konklusjoner. 

Som referanser for videre diskusjon og kommentarer, se fotnote².

Økonomiske hypoteser

I analyseperioden 2001–2022 har både Norge og EU-landene hatt flytende valutakurser. I analysen kan vi derfor ignorere valutakurssystemet som forklaringsvariabel på kronekursutviklingen – og i stedet konsentrert oss om variablene nedenfor.

Tidligere valutakurs

Det er rimelig å tro at aktørene i valutamarkedet ser seg bakover i tid og observerer historiske valutakurser når de skal tilpasse seg i valutamarkedet, og at dette vil indirekte påvirker kursutviklingen videre. Hypotesen er at hvis valutakursen i snitt har styrket seg under de siste observasjoner, så vil det være en faktor som styrker valutakursen – og omvendt. Dette går blant annet fram av Bernhardsen og Røiseland (2000), Bjørnland og Hungnes (2006), Aamodt (2009) og Vale (2018).

Høyere oljepris

Høyere oljepris øker verdien av oljeselskapene som er notert på Oslo Børs. Investorer med ledig kapital vil nå vurdere å kjøpe seg inn/opp i disse selskapene. Da vil kronekursen styrke seg.

En supplerende forklaring er at en høyere oljepris vil gi Norge (og andre oljeproduserende land) et gunstigere bytteforhold overfor utlandet. Det vil gi større eksportoverskudd – som igjen vanligvis vil øke nettoetterspørselen etter norske kroner – med styrket kronekurs som resultat.

Forskning bekrefter også at økt oljepris styrker kronekursen. Senest Akram (2019) og Klovland mfl. (2021) og har vist dette. Bjørnland og Hugnes (2006; 2007), i en tidlig fase av norsk oljeøkonomi, fant ingen slik sammenheng mellom oljepris og kronekurs. Akram (2000; 2001; 2019) viste at effekten av en stigende oljepris avhenger av nivået på oljeprisen, et funn som gjør det mulig å akseptere begge de sprikende resultater nettopp nevnt: Er oljeprisen i utgangspunktet relativt lav (som den var tidlig på 2000 tallet), er effekten av en økt oljepris på kronekursen liten, den er større når oljeprisen er på et relativt høyt nivå (som den var rundt 2020).

Denne dobbeltheten i sammenheng mellom oljepris og valutakurs finner vi også i Figur 2. Vi ser at den langvarige og markante oljeprisstigning etter 2001 ikke gir en sterkere valutakurs (den holder seg stort sett på samme nivå). Heller ikke da oljeprisen tok seg opp igjen i 2016/17 etter fallet i 2014, styrket kronen seg. Derimot, og et resultat som bekrefter dobbeltheten, vises i Figur 2 ved at den økte oljepris fra 2009 styrket kronekursen. 

En konklusjon av Figur 2 vil være at kronekursen nok kan henge sammen med oljeprisen, men det må også være andre forhold som påvirker valutakursen.

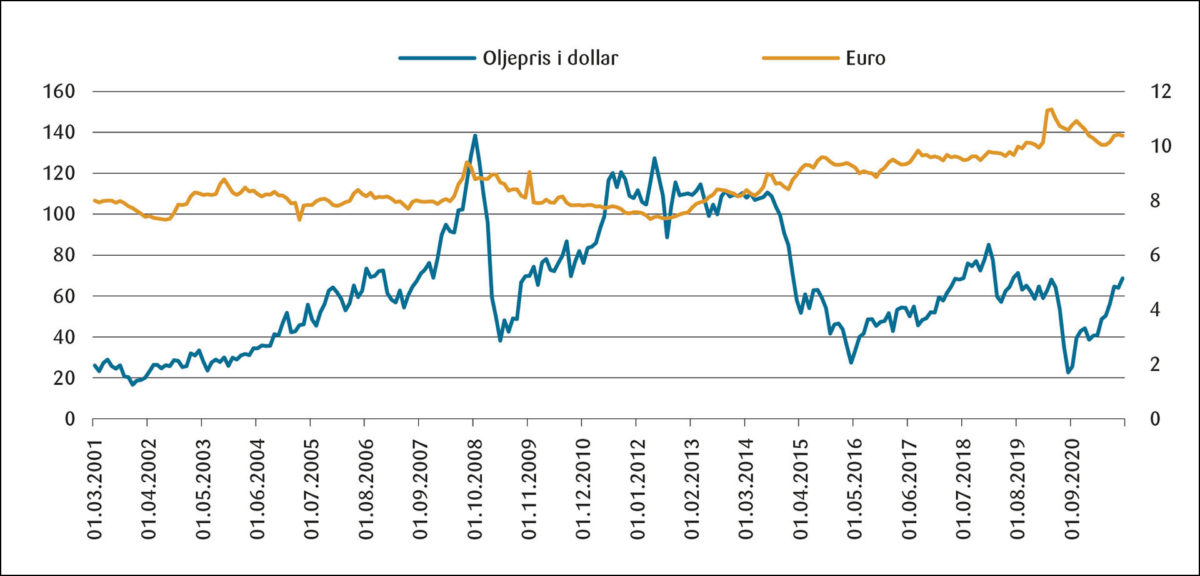
Konsumprisdifferanser – kjøpekraftsparitetshypotesen 

Kjøpekraftsparitetshypotesen tar sitt utgangspunkt i loven om en pris: Altså at en vare koster det samme – uansett sted og tidspunkt for handelen. Dette vises i likning (1a) nedenfor. Venstre side av likningen viser hva vi i Norge må betale når vi handler i EU-området. Høyre side viser prisen nordmenn betaler når de handler hjemme i Norge. Hvis de to prisene skal være like, må det være likhetstegn mellom dem. 

E P^* = P_N(1a)

eller 

R = E P^* / P_N = 1(1b)

hvor

E er nominell verdi av norske kroner (mot euro).

P^* er den harmoniserte konsumprisindeks i EU.

P_N er konsumprisindeksen i Norge.

R er realvalutakurs.

Venstre side i likning (1b) definerer realvalutakursen. Vi forstår av høyresiden at realvalutakursen viser forholdet mellom prisen i EU-området og i Norge. Under kjøpekraftsparitetshypotesen må følgelig realvalutakursen være 1.

Vi skal senere undersøke om kjøpkraftsparitetshypotesen gjelder, og vi skal da undersøke om realvalutakursen er 1.

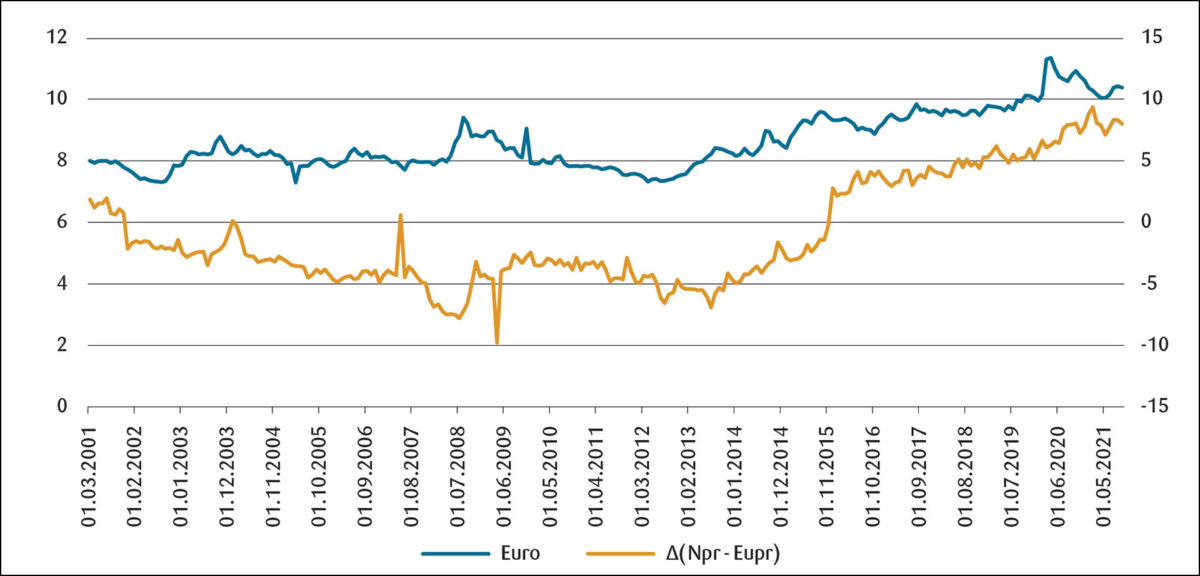
Figur 3 viser utviklingen i kronekursen mot euro, og endringer i differansen mellom konsumprisen i Norge og EU. Det er grovt sett ganske stor parallellitet i bevegelsene. Det kan indikere at det er sammenheng mellom valutakursen og prisdifferanser. Hvis prisen i Norge stiger raskere enn i EU, slik som for eksempel etter 2014, så ble kronekursen svekket. Omvendt, hvis prisen i EU stiger raskest, slik som i perioden 2010–2014, styrket krona seg. Vi ser også at kronekursen endrer seg uten at det kan ha sammenheng med utviklingen i prisene.

Det fleste studier forkaster kjøpekraftsparitetshypotesen, blant annet Bjørnland og Hungnes (2002; 2006), Bernhardsen (2008) og Klovland mfl. (2021). Dette er ikke overraskende med tanke på de krevende forutsetninger som ligger bak hypotesen;

• Ubetydelige transportkostnader og at varene ikke påføres avgifter på reisen mellom kjøper og selger. 
• Forbrukerne skal ikke ha varierende betalingsvilje for varer fra eget land og andre land.
• Enkelte tjenester – medisinske, barnehaver, frisører m.m. – er noen ganger ikke mulig å handle fra andre land og representerer derfor et brudd på PPP-hypotesen.
• Monopol og markedsmakt muliggjør prisdiskriminering som også er uforenlig med kjøpekratsparitetshypotesen.

Renten

Ved en høyere rente i Norge vil aktører i det globale finansmarked med ledig kapital overveie å flytte penger til Norge for å få en høyere avkastning på sin kapital. Det vil også norske aktører gjøre som har en kortsiktig plassering i utlandet. Dette vil i tilfelle øke nettoetterspørselen etter norske kroner – og kronekursen vil styrke seg. 

Flere norske studier viser at relativ høyere norsk rente styrker krona, blant annet Bjørnland og Hungnes (2006), Bjørnstad og Jansen (2006), i senere tid Adrid (2018) og Klovland mfl. (2021). 

Figur 4 nedenfor viser kurven for kronekursen (øverst) og gapet mellom 3 måneders Nibor og Euibor rentene i analyseperioden 2001–2021. Vi ser at da dette rentegapet økte kraftig i 2002 – og senere samme år falt mye – styrket og henholdsvis svekket kronekursen seg i samsvar med hypotesen. Noe liknende skjedde da rentegapet ble redusert i 2008 og i 2020. I perioden 2013–2017 gikk rentegapet ned, og kronekursen svekket seg.

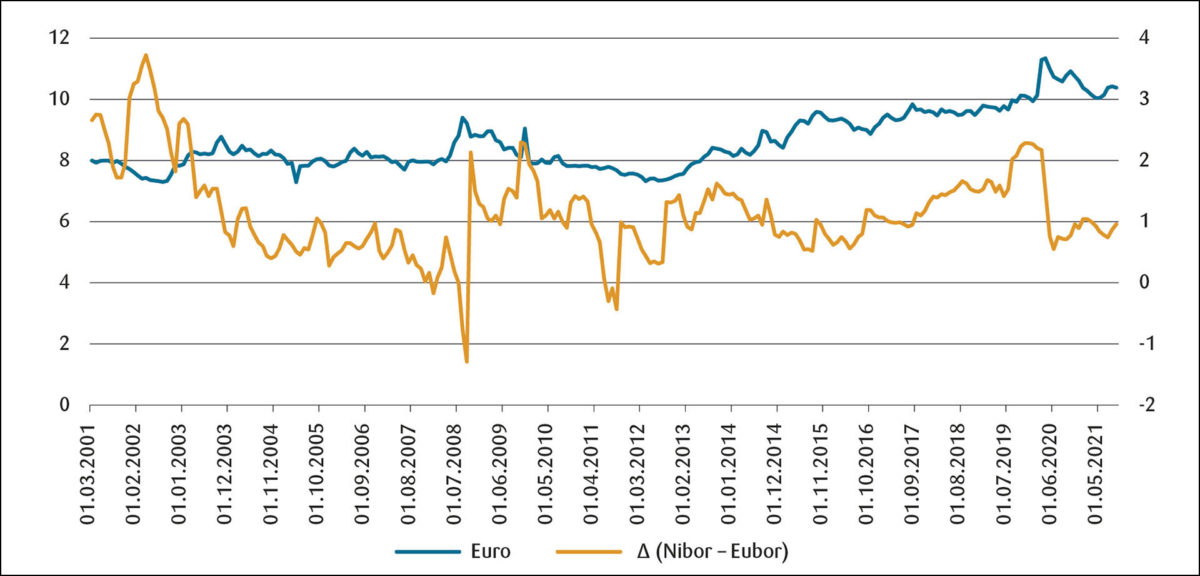
Ellers sank rentegapet i perioden 2002–2007 uten at det synes å slå ut på kronekursen. 

Turbulent konjunkturutvikling

Det vil være rimelig å anta at aktørene i aksjemarkedet vil være påvirket av forventet stabilitet / uro i valutamarkedet når de foretar sine valutadisposisjoner. VIX-variabelen³ er en populær indeks for å spore volatilitet på USAs aksje-marked og forventninger om den videre utvikling. Dette aksjemarked har stor betydning for alle andre aksjemarkeder. En mulig hypotese er derfor at hvis denne indeksen er høy (som reflekterer usikker konjunkturutvikling), vil aktørene i valutamarkedet være varsomme med å plassere penger i en liten og usikker valuta som den norske. Til gjengjeld vil det kanskje være en tendens til å kronekursen vil styrke seg i internasjonalt gode tider. Som vi senere skal vise, hadde denne variabelen ingen betydning for kronekursen.

Når det gjelder dette siste resultatet, er det hevdet at de store overskudd i norsk utenriksøkonomi og betydelige finansielle muskler i Pensjonsfond Utland har bidratt til å gjøre den norske krone robust overfor konjunkturusikkerhet. 

Finanskrisen m.m. 

Finanskrisen i 2008 kom helt overraskende. Den påvirket definitivt økonomien og valutakursene, herunder kronekursen (se senere). Det er ikke mulig for de økonomiske aktørene og myndighetene å ta hensyn til slike «overraskende hendelser», når de skal planlegge/foreta sine valutadisposisjoner. Forskere kan imidlertid i ettertid innføre og definere disse begivenheter som sjokkvariable og bruke dem i empiriske studier for på den måten å forebygge at effektene feilaktig forstås som konsekvenser av andre forklaringsvariabler. 

I tillegg til finanskrisen, skal vi definere to andre sjokkvariabler som var aktive i perioden vi studerer:

• EUs bankkrise – fra 2011/2012 fram til 2014. 
• Oljeprissjokket, da oljeprisen i 2014/2015 falt kraftig helt overraskende.

En økonomisk modell

Den økonomiske analysen av kronekursen mot euro skal som sagt skje med den feilkorreksjonsmodellen som er spesifisert i likning (2) nedenfor. Det er allerede nevnt en hovedgrunn for dette valget; modellen gjør det mulig å estimere den langsiktige likevekten i valutakursen. I tillegg kan modellen gjør det rimelig enkelt å tolke de forskjellige parameterne (som lett kan bli et problem i andre dynamiske modeller). For det tredje har denne økonomiske modellen vist sin kvalitet ved å gi valutaprognoser som overgår RW-modellen, Ca` Zorzi, M., mfl. (2016).

Høyreside variablene i likning (2) ble varslet i forrige kapittel. Variablene har i likning (2) fått form av laggede variabler; laggede verdier av valutakursen, av gapet mellom norske priser og EU priser, av gapet mellom norske renter og EU renter, av oljeprisen, og av variabelen som viser risikoen på verdensmarkedet. Grunnen til den laggede formen skyldes at vi har hatt månedsobservasjoner (se senere avsnitt om data), og det er rimelig å anta at effekten av de nevnte uavhengige variablene ikke vil være uttømt i løpet av en måned, men ha påvirkning i etterfølgende perioder. Det betyr at spot valutakurs på tidspunkt t vil bli avhengig av laggede variabler datert t-1, t-2, t-3 osv.

Braketten, til slutt i ligningen, viser en dynamisk effekt på nominell valutakurs av at det er et avvik mellom spot kronekurs mot euro og langsiktig likevekt for kursen (som framkommer når vi setter ΔE,_t = 0). Parameter ɵ₁ angir hvor raskt et avvik mellom spotvalutakurs og langsiktig likevekt vil bli eliminert – og at det igjen blir likevekt.

E_t = a + Σ_i b_i ΔE, _t-j + Σ_i c_i Δ(P_N – P_EU),_t-1
+ Σ_i d_i Δ(i_N – i_EU), _t-j + Σ_i f_i Δolje pris,_t-j

+ Σ_i g_i ΔVIX,_t-j + ɵ₁[E, _t-1 – {(P_N,_t-1 – P_EU,_t-1) 
+ ɵ₂ (i_N – i_EU), _t-1 + ɵ₃ Oljeprise, _t-1
+ ϴ₄ VIX, _t-1, + Σ_i λ_i, Q_i}] + ɛ_t(2)

hvor

E_t = Nominell kronekurs mot euro på tidspunktet t.

Δ E_t = Endring nominell kronekurs mot euro på tidspunktet t.

Δ (P_N – P_EU),_t-1 = Endring i differensen (P_N – P_EU) på tidspunkt t-1.

Δ (i_N – i_EU), _t-i = Endring i differensen (Nibor -Euribor). på tidspunkt t-1.

Oljepris, _t = log Oljepris på tidspunkt t

Δ Oljepris, _t-i = Endring i log Oljepris på tidspunktet t-1. 

VIX, _t-1 = indikator for voalitet på USAs aksjemarked t-1.

– Q_h = Ulike sjokk; h=1: finanskrise, h=2: EUs bankkrise og h=3: Oljeprissjokk

– ɛ_t = Et stokastisk restledd

a, b, c, d, e, f, g, ϴ₁ … ϴ₅ samt λ er ukjente koeffisienter

Langsiktig likevekt for valutakursen, som vi altså finner ved å sette endringsvariablene i ligning (2) lik null, kan da uttrykkes som i ligning (3) nedenfor. Dette blir hovedmodellen i den påfølgende analyse og diskusjoner. Ved å estimere likning (3) vil vi finne påvirkningen de uavhengige variablene har på denne likevektskursen – og hvor sterk den er.

Hvorvidt denne langtidslikevekten er en sann likevektssituasjon for valutakursen, kan vi likevel ikke påstå helt sikkert siden vår modell fortsatt er en submodell (en kan lett tenkt seg at andre funksjonsformer og også andre variabler kunne hatt betydning for valutakursen). I det videre skal vi imidlertid teste modellen for slike momenter, blant annet ved en reset test som tester om en annen funksjonsform enn den lineære kunne vært bedro.

Det er som tidligere sagt parameter ɵ₁ i likning (2) som bestemmer hvor raskt valutakursen konvergerer mot sin langtidslikevekt. Studier, blant annet av Bernhardsen og Røiseland (2000) og Vale (2018), har vist at det kan ta 13 henholdsvis 16–17 måneder fra en gitt likevekts situasjon, får en ny likevekt.

E_t = α + ϴ₁ (P_N, _t-1 – P_EU, _t-1) + ϴ₂ (i_N – i_EU), _t-1 + 

ϴ₃VIX_t-1, + ϴ₄Oljepris, _t-1 + Σ_i λ_i,Q_i + ɛ_t(3)

Data ved estimering 

Data er månedsobservasjoner av variablene i likning (3) i perioden 01.03.2001 – 09.2021, i alt 244 uavhengige observasjoner. Disse observasjonene glatter ut noe av variasjonen i valutakursen som det i års data kunne vært vanskelig å forklare.

Prisen i Norge er representert med konsumprisindeksen (CPI). Som pris i EU-området er brukt den harmoniserte konsumprisindeksen. Rentene i Norge er representert med de månedlige observasjoner av 3-måneders renten Nibor, og i EU de månedlige observasjoner av 3-måneders renten Eubor. Oljeprisen i modellen er satt lik Brent Blend Crude Price. Turbulens variabelen VIX er satt lik den månedlige observasjon av Chicago Board Exchange Volatilitet Index. 

Vi har i beregningene brukt de absolutte variable observasjoner. Begrunnelsen er at dette gir en analysemodell som er veldefinert når det gjelder standard modell krav, se f.eks. Tabell V-1 i et vedlegg. Dette valget har imidlertid den konsekvens at det er noe vanskeligere å sammenligne de empiriske resultater med andre studier hvor en bruker log transformerte variabler og beregner prosentvis endring i kronekursen per prosentendring i de uavhengige variabler. 

Test og metoder for å vurdere beste modell

Vi vil først teste om det er den økonomiske modellen i likning (3), eller om det er likning (4) som er vår representant for RW-modellen, som best forklarer kronekurser. Likning (4) sier at kronekursen på tidspunkt t er lik siste observasjon (N_t-1). Vi har utvidet denne enkle RW-modell med et trendledd som skal fange opp endringer valutamarkedet som f.eks. skyldes norsk oljerikdom, nye tendenser i dollar / euro forholdet. 

E_t = N_t-1 + δT + ɛ_t.(4)

hvor 

E_t er nominell valutakurs på tidspunkt t

T er en tidsvariabel

δ er trendledd

ɛ_t. er stokastisk restledd

Hvis vi forklarer E_t med høyreside variabler både fra likning (3) og (4), får vi likning (5). 

E_t = α + (P_N, _t-1 – P_EU, _t-1) + ɵ₂ (i_N – i _EU), _t-1 + ϴ₃VIX_t-1, 

+ ɵ₄Oljepris, _t-1 + Σ_i λ_i,Q_i + + αN_t-1 + δT + ɛ_t(5)

«Discerning approach» sier at vi kan teste om den økonomiske modellen i likning (3) er bedre / dårligere teori enn RW-modellen i likning (4) ved å estimere likning (5), se Gujarati og Porter (2008). Hvis signifikante parametere i likning (3) nå ender opp som ikke-signifikante, mens variablene i likning (4) fortsatt er signifikante, indikerer dette at RW-modellen vil ha en forklaringskraft utover den økonomiske. I det omvendte tilfelle, vil den økonomiske modellen være best.

Gujarati og Poster (2008.) viser at slike konklusjoner bygger på krevende forutsetninger, blant annet at variabelvektoren i likning (3) ikke må være korrelert med variabelvektoren i likning (4). Ikke minst problematisk er det at resultatet vil avhenge av hvilken av modellene som vil bli brukt som referanse hypotese. Dette siste betyr at testen vil gi usikre resultater. Vi vil derfor også vurdere andre metoder for å kunne få tryggere konklusjoner.

Andre metoder

En alternativ metode for å avgjøre hvilken modell som er best, vil være å beregne kronekursprediksjoner på grunnlag av de estimerte modellene, og som vi plotter inn i en graf. Sammen med kurven for de faktiske valutakursnoteringer vil dette gi et visuelt bilde av feilmarginene til prediksjonene og gi en indikasjon på hvor gode prognosene er. Slike kroneprediksjonene for likningene (3) og (4) vil bli konstruert ved et spesielt program «forecast» i regneprogrammet PC-Give. 

Vi har i våre vurderinger tatt hensyn til at det kan bli vanskelig fra disse grafene å trekke entydige konklusjoner om beste prediksjon. I dette tilfelle har vi søkt hjelp med det matematiske uttrykket Root Mean Square Error (RMSE), som er et eksakt mål på avviket mellom prediksjonene og observasjonene. Formelen for RMSE er vist i likning (6).

RMSE = $\sqrt{\mathrm{1/n<munderover><mo>\sum <mi>t=1n</mi>(<mi>NokEuro, t-NokEuro,t*</mi>)2</mo></munderover>}}$​     6)

hvor

​ $NokEuro, t=observert kronekurs$​

​ $NokEuro,t*$= kronekurs prediksjon

Et ytterligere kriterium for å evaluere kvaliteten på kronekursprediksjonene er å se på grafen for kronekursprediksjonene om valutakursendringer, oppover, nedover eller nivåkonstant, inntreffer i samsvar med den observerte valutakurs. Dette er sjekket ved å bruke øynene om kronekursprediksjoner med den økonomiske modellen treffer endringene bedre enn RW-prognosen.

Hva viser «Discrimination approach»

Resultatene da vi estimerte likning (5) med minstekvadraters metode er vist i Tabell 1.

Tabell 1: Estimering av likning (5).

Variabel	Parameter	T-verd
Konstant	0,394	1,382
(Pris N – Pris EU)	-0,006	-0,758
(Nibor – Euibor)	0,014	0,709
Oljepris	-0,0007	-0,905
VIX	-1.6586e-006	-0,905
finanskrise	-0,073	-1,102
Bankkrise	-0,039	-0,559
Oljeprissjokk	-0,033	-0,602
N-1	0,945	29,490
Trendledd	0,00097	2.2536

Vi ser at (Pris N – Pris EU), (Nibor – Euibor) og oljeprisen ikke er signifikante, men som vi skal se at de var da vi estimerte likning (3) (se Tabell 4 side 18). Dette kan antyde at RW-modellen har en forklaringskraft på valutakursen som går utover det som den økonomiske modellen har. Resultatet kan isolert styrke RW-modellen vis a vis den økonomiske modellen. Men med de restriktive forutsetninger som denne testen forutsetter, er det er vanskelig å utrope RW-modellen som en vinner. Derfor vil vi gå videre og bruke de alternative metoder / kriterier som er vist ovenfor.

Utledning av kronekursprediksjoner 

Først må vi estimere modellene og finne fram til hvilke variabler som påvirker kronekursen. For å unngå spuriøse estimater ved estimering av den økonomiske modellen i likning (3), dvs. falske estimater påvirket av andre variabler enn de som er spesifisert, har vi sjekket at variablene i modellen er stasjonære. Vi har testet denne forutsetningen med en Augmented-Dickey Fuller-test, med et driftsledd spesifisert som likning (6). Nullhypotesen er at modellen har enhetsrøtter som forkastes når T-verdien er (vesentlig) lavere enn sikkerhetskravet på 5 prosent. Testresultatet er vist i Tabell 2.

Δy_t = α+βt + γ y_(t−1) + δ1Δy_(t-1)
+ δ2Δy_(t-2) + … + δ1Y Δy_(t-p) + ε_t(6)

Tabell 2: Resultater av ADF-test om stasjonaritet.

Variabel	T-ADF	5 % sikkerhetskrav
Kronekurs	-0,867	-2,87
(Pris N – Pris EU)	-0,104
(Nibor – Euibor)	-3,782**
Oljepris	-2,413
VIX	-9,022**

Tabell 2 indikerer at (Nibor – Euibor) og VIX-variabelen er stasjonære. Vi antar at finanskrisen, bankkrisen og oljeprissjokket som er dummy variabler også er det. Derimot oppfyller ikke prisgapet (Pris N – Pris EU) og oljeprisen dette kravet. For å estimere likning (3) uten å unngå spuriøse estimater kan vi nå enten differensiere de ikke-stasjonære variablene eller bruke kointegrerte variabler. Ved å differensiere de ikke-stasjonære variablene vil vi estimere de kortsiktige sammenhenger. Når vi skal sammenlikne den økonomiske modellen og RW-modellen, skal vi teste ved hjelp av den langsiktige likevektsløsningen for kronekursen. Vi har derfor på spørsmålet ovenfor om variabeltype, svart kointegrerte variabler. 

Er variablene i likning (3) kointegrerte?

Dette spørsmålet er undersøkt ved at vår hovedmodell likning (3) ble estimert ved minste kvadraters metode, samtidig som residualene ble tatt vare på, og deretter testet for stasjonaritet ved en ADF-test. Testresultatet går fram av Tabell 3.

Tabell 3: Testresultat om variablene i likning (4) er kointegrerte.

Variabel	Testresultat	5 % sikkerhetskrav
Residualene da likning (3) ble estimert)	-4,582	-2,87

Testresultatet i Tabell 3 innebærer at residualene er stasjonære og at variablene i likning (3) er kointegrerte. Vi har herfra sluttet at vi kan estimere likning (3) ved minste kvadraters metode uten at å risikere spuriøse resultater.

Hva påvirker kronekursen?

Da likning (3) ble estimert med minste kvadraters metode fikk vi resultatene i Tabell 4⁴.

Tabell 4: Estimatene for parameterne i likning (3)

Variabel	Parameter verdi	T-verdi	P-sannsynlighet
Konstantledd	8,40	82,4	0,00
(Pris N – Pris EU)	0.09	6,44	0,00
(Nibor – Euibor)	-0,16	4,11	0,00
Oljepris	-0,01	4,34	0,00
VIX	9,21e-006	0,97	0,37
Finanskrise	0,67	5,27	0,00
EU-bankkrise	-0,16	-1,11	0,29
Oljeprissjokk	-0,00	-0,03	0,98
Trendledd	0,01	9,05	0,00

Tabellen 4 viser at kronekursen mot euro blir påvirket av konsumpris gapet til euro, 3-måneders rente gapet, oljeprisen, finanskrisen og trendleddet. Alle fortegnene er i samsvar med hypotesene.

Kronekursprediksjoner med den økonomiske modellen

Kronekursprediksjoner ble konstruert på grunnlag av signifikante estimater i likning (3), se Tabell 4. Vi tok heller ikke med dummy variabelen for finanskrisen, som var en isolert historisk hendelse og som med liten sannsynlighet ville komme tilbake i prognose perioden. 

Prediksjonene ble fortatt ved hjelp et PC Give regneprogram, meny «forecast». Ved beregningene tok vi til side et visst antall kronekursobservasjoner, som vi ville bruke i en kvalitetskontroll av prediksjonene, se nedenfor og Figur 5.

Det ble utarbeidet prognoser med forskjellige tidshorisonter: En periode var på 24 måneder og en annen litt lengre var på 48 måneder, med formål å teste om de to modeller hadde ulike egenskaper når vi varierte prognosehorisonten. 

Den praktiske gjennomføringen av prediksjonene var denne: For tidshorisonten på 24 måneder ble prognosemodellen estimert på basis av de første 220 observasjoner (av de i alt 244). Da ble da tilbake 24 faktiske observerte kronekurser som vi kunne sammenlikne med våre kronekursprognoser som kvalitetskontroll. Ved 48 måneder prognosen ble modellen estimert på basis av de første 196 observasjoner, og det var tilbake 50 observerte kronekurser til kvalitetskontrollen.

På en helt analog måte ble det laget kronekursprediksjoner på grunnlag av den estimerte RW-modellen i likning (4).

Hva viser grafene?

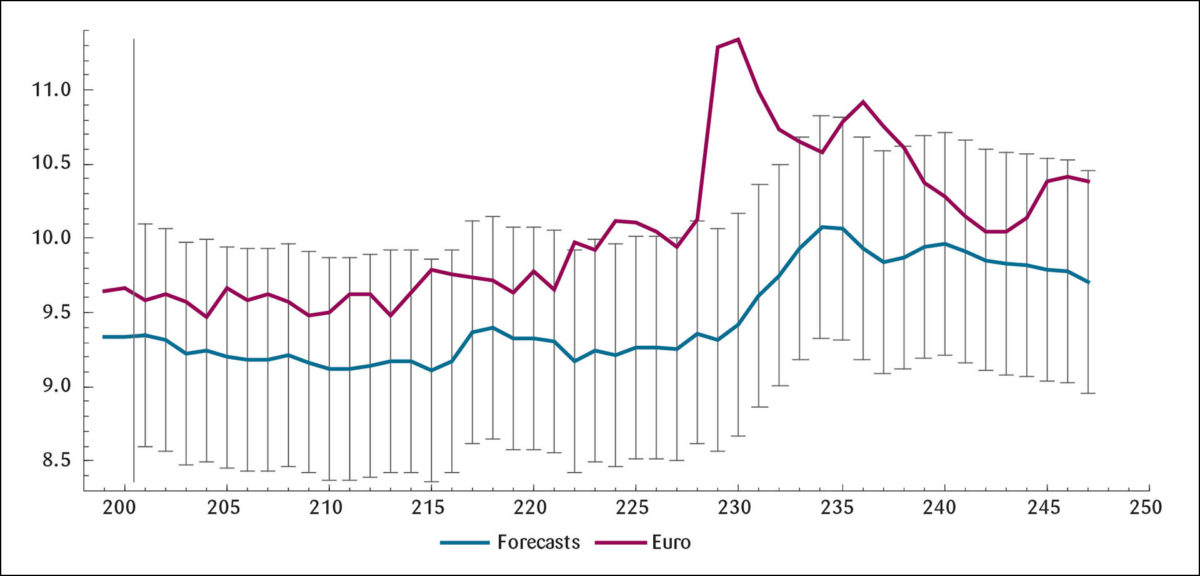
Figur 5 viser grafen for valutkursprediksjoner med en horisont på 24 måneder med den økonomiske modellen. I figuren er også inntegnet de faktiske krone-kursobservasjoner, nærmere bestemt for perioden 220–244 (årene 2019–2021). Den første tiden danner prediksjonene en kurve relativt tett under kurven som de observerte valutakurser danner. I uke 228 øker klart avviket mellom kurvene fram til uke 230 da avviket er på sitt største. Dette tidspunktet er mai 2020, og kronekursen er rekordsvak og passerer 11 krone. Forklaringen på den svake krone er et kraftig oljeprisfall, se Figur 2, og at det på denne tiden var en relativt usikker makroøkonomisk situasjon i Norge. Deretter avtar gapet og prognoser og observert verdi nærmer hverandre, og i måned 240 krysser er de hverandre. Gapet mellom kurvene før uke 228 og etter uke 230 er relativt moderat, vel 4–5 prosent og lavere, 

Hvis vi sammenligner med RW-prediksjoner i Figur 7 (nederst på siden), ser vi at RW-modellen heller ikke klarer å forutsi kronesvekkelsen uke 228/mai 220. Men med det blotte øye kan det kanskje se ut til at RW-modellen ligger nærmere de observerte kronekurser. 

Den siste påstanden bekreftes av de beregnede RMSE-verdier i Tabell 5 nedenfor, som for 24 måneders horisonten klart går i favør av RW-modellen..

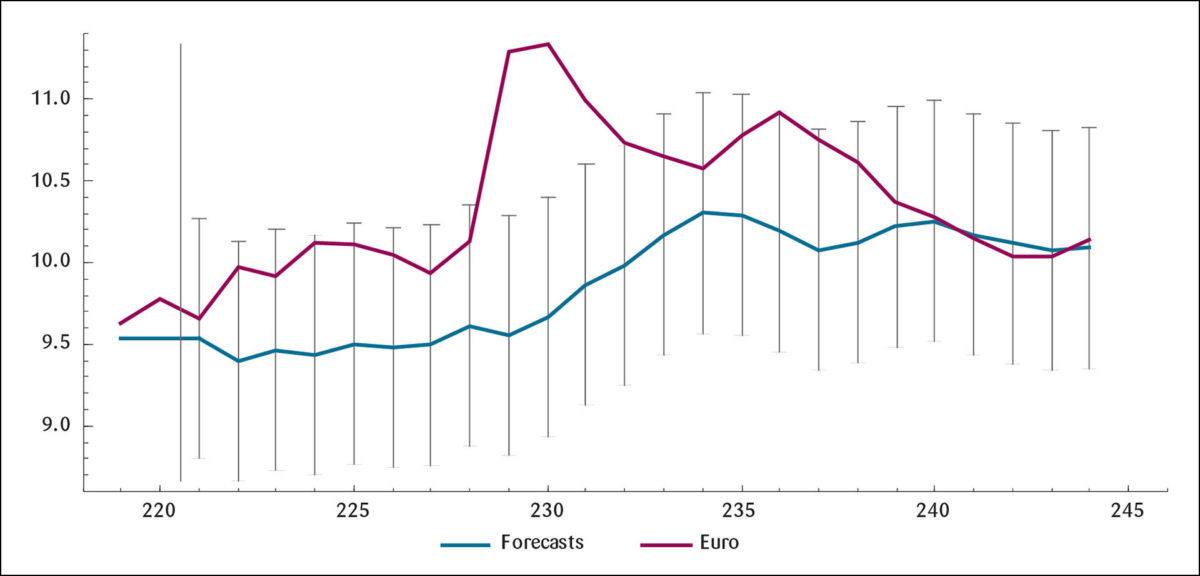
Figur 6 viser prediksjonene når den økonomiske prognosemodellen har en horisont på 48 måneder og strekker seg fra måned 200 til måned 244 (årene 2017–2021). Kurven for prediksjonene ligger også nå litt under kurven som de observerte kronekurser danner. I gjennomsnitt for hele 4 års perioden er avviket vel 4 prosent. 

Når en kommer til måned 228 og det store oljeprisfallet, svekker den faktiske kronekursen seg betydelig, men som den økonomiske modellen ikke fanger opp.

Det er interessant – og en styrke ved den økonomiske modellen – at den et stykke på vei simulerer svingningene i den observerte kronekursen, riktignok med en viss forsinkelse.

Hvis vi går til RW-beregningene for en horisont på 48 måneder i Figur 8 på neste side, er RW-modellen blottet for en slik evne. Avviket til den faktiske kronekurs er heller ikke nevneverdig mindre med RW-modellen, se Tabell 5. Legger vi størst vekt på modellens evne til å simulere svingninger (med et visst lite lag), kan den økonomiske modellen nå til en viss grad konkurrere om å være best.

RMSE- beregningene

RMSE-beregningene i Tabell 5 kårer RW-modellen som vinner når prognose-horisonten er 24 måneder. 

Konkurranseforholdet er jevnt mellom modellene når prognoseperioden endres til 48 måneder og vi betrakter disse grafer og RMSE-beregningene under ett. 

Legges det vekt på egenskapen å forutsi når valutakursutviklingen endrer retning, kan konklusjonen under stor tvil bli at den økonomiske modellen kan vinne.

Tabell 5: RMSE-beregninger for den økonomiske modell og RW-modellen.

Modell	24 måneder	48 måneder
	RMSE	RMSE
Økonomisk modell	0,74887	0,70909
Random – Walk modell	0,5358	0,77258

Kronekursprediksjoner med RW-modellen.

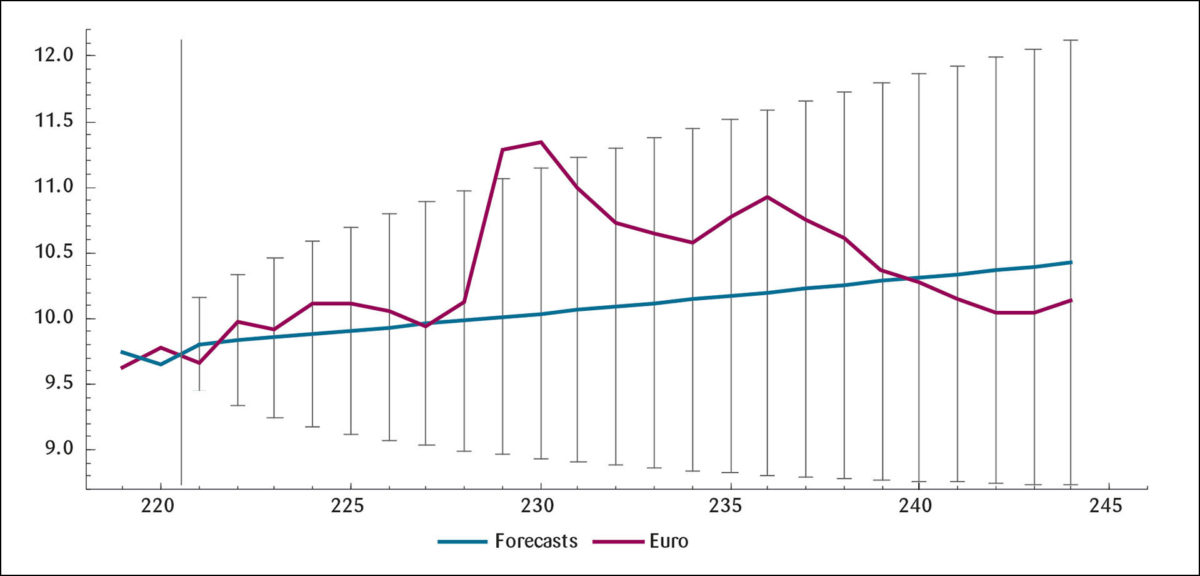
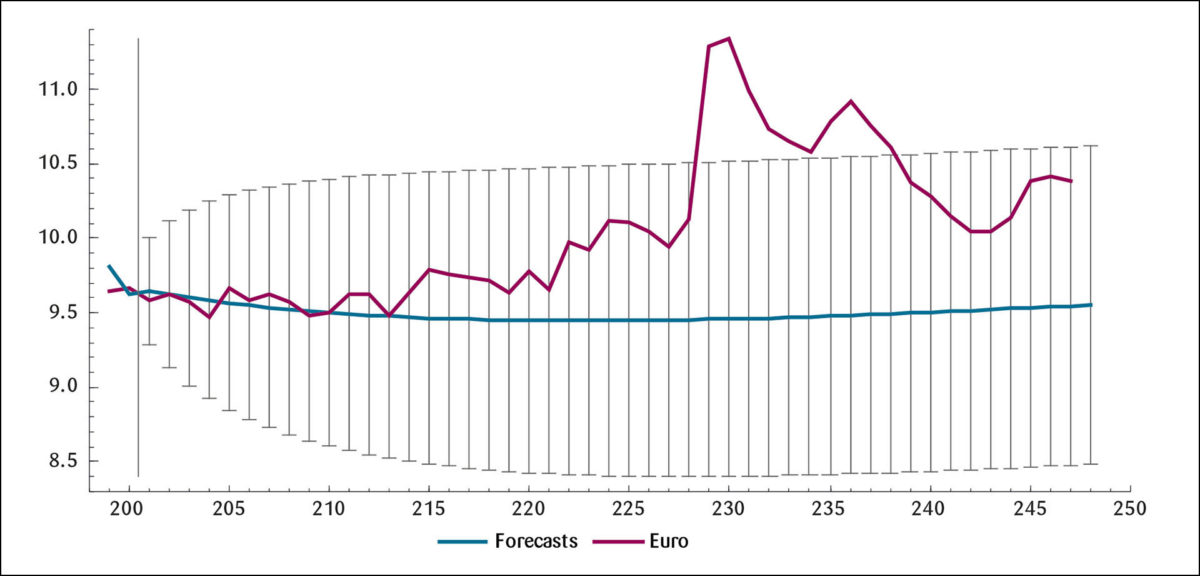
Konklusjoner 

Da vi testet den økonomiske modellen versus RW-modellen med Discerning approach, antok vi forutsetninger som ikke uten videre var oppfylte. Det er derfor vanskelig å konkludere med annet enn at testen gav en viss støtte til RW-modellen. 

Den økonomiske modellen kjemper tappert i den grafiske framstilling mot RW-modellen i alternativet med en planhorisont på 24 måneder. Begge modellene har felles at de ikke fanger opp den kraftige kronesvekkelsen mai 2020. Det er ikke lett med det blotte øyet å se om det i modellene er nevneverdige forskjeller mellom predikert og observert valutakurs. Det er forskjellen i RMSE-verdien i Tabell 6 som gjør at vi nå må kåre RW-modellen som litt bedre. 

Hvis vi går over til prognosene med en 48 måneders horisont, viser RMSE-beregningene at den økonomiske modellen og RW-modellen nå er jevngode. Heller ikke disse modellene evner en å forutse den svake kronekursen mai 2020. Derimot kan den økonomiske modellen antyde litt om tidspunktene når kursutviklingen endrer retning (med et lite lag). Dette kan være viktig kunnskap for aktørene i valutamarkedet. Legges meget stor vekt på denne egenskapen, kan den økonomiske modellen ved en planleggingshorisont på 48 måneder kåres som svak vinner.

Hovedkonklusjonen blir: Selv om det er mindre forskjeller i konsekvensene av å bruke modellene, er det likevel vanskelig å utrope en klar vinner.

VEDLEGG: TESTER AV DEN ØKONOMISKE MODELLEN

Test av standard tester for den økonomiske modellen i likning (3). 

Likning (3) er her testet for autokorrelasjon, normalfordelt restledd, heteroskedastisitet og spesifikasjonstest (reset).

Tabell V-1: Test om likning (3) er veldefinert

Test type	Test resultater
AR 1-2 test	1,9814 (0,1439) **
ARCH 1-1 test	0,4103 (0,0028)
Normalitet test	134,08 (0,000) **
Hetero Test	1,9585 (0,0415) **
Hetero-X test	1,9056 (0,0227) **
Reset test	0,2759 (0,6005) **

Tabell V-1 viser at modellen er veldefinert og oppfyller de fleste kravene som en ønsker å stille til en slik økonometrisk modell. ARCH 1-1 oppdager kanskje autokorrelasjon i residualene som AR 1-2 ikke har klart å fange opp. Vi ser videre at vi ikke kan forkaste hypotesen at residualene er normalfordelt. Heller ikke kan vi forkaste at residualene har konstant varians. Reset testen indikerer at andre funksjonsspesifiseringer vil gi noe bedre resultat. 

Multicollinearitet

Resultatet av korrelasjonsberegningene er vist i Tabell V-2. Tabellen beskriver 5 nivågrupper for korrelasjonskoeffisientene. Av de 73 korrelasjonskoeffisienter som ble beregnet (forskjellige fra 1), havnet 68 prosent i korrelasjonsgruppen 0–0,20 og 10 prosent i gruppen 0,20–0,30. Det betyr at en ubetydelig andel korrelasjonskoeffisienter er over 0,50, og en kan telle på en hånd de over 0,80. Vi kan slutte at problemet med multicollinearitet er helt, helt ubetydelig.

Tabell V-2: Korrelasjonskoeffisienter, i absolutte tall, fordelt på grupper etter stigende korrelasjonsnivå.

Antall korrelasjonskoeffisienter	50	10	4	4	3
Korrelasjonsnivå.	0–0,20	0,20–0,40	0,40–0,60	0,60–0,80	0,80–1,00

Kjøpekraftsparitetshypotesen

Kjøpekraftspritetshypotesen påstår at en vare koster det samme uansett sted og tidspunkt. Som forklart tidligere kan denne hypotesen bli undersøkt ved å teste om realvalutakursen er stasjonær. 

Ved en ADF-test fikk vi de empiriske resultatene i Tabell V-3. Konklusjonen her er at vi må forkaste kjøpekraftsparitetshypotesen. Et resultat nesten alle norske studier av spørsmålet har fått.

Tabell V-3: ADF test av realvalutakursen.

Variabel	T-ADF	5 % sikkerhetskrav
R (realvalutakurs)	-2,321	2,87

Fotnoter:

1. Takk til Marius Stornes, Kyrre Richardsen, Ole Gjølberg samt anonym fagkonsulent. ↩︎
2. Reiten og Omnegene (1999), Eitrheim mfl. (1999), Akram (2002; 2003; 2019), Bernhardsen og Røiseland (2000), Bjørnland og Hungnes (2002; 2006), Naug (2003), Kloster mfl. (2003), Bjørnstad og Jansen (2006; 2007), Aamodt (2009), Flatnes (2009), Gimmingsrud (2012), Kj (2015), Gogas og Plakandaras (2016), Adrik (2016), Vale (2018), Henanger og Scjerpen (2018) og Klovland mfl. (2021). ↩︎
3. Vårt symbol for Chicago Board Options Exchanges Volatilitet Index. ↩︎
4. I et vedlegg er det referert til andre tester som ble foretatt av den økonomiske modellen i likning (3), blant annet en mht standard egenskaper som nomalitet test, AR 1-2 test, Hetero Test m.m. Vi har også testet for multicollinearitet samt kjøpekraftsparitet. ↩︎