Optimale handlingsregler¹

Introduksjon

Den siste tiden har flere tatt til orde for at handlingsregelen bør justeres (Henriksen, 2022; Hoel og Qvigstad, 2023; Holden, 2022; Mork mfl., 2022; Wulfsberg, 2022). Felles for mange av bidragene er at avkastningsrisiko er problematisk og at dette må håndteres ved å redusere det årlige uttaket fra Statens Pensjonsfond Utland (SPU). I denne artikkelen presenteres et rammeverk for å tenke på hvordan flere ulike relevante faktorer spiller en rolle for utformingen av handlingsregelen. Mitt håp er å bidra med en prinsipiell tilnærming til utformingen av handlingsregelen. 

Modellen følger et standard rammeverk fra konsumentteori. En sosial planlegger maksimerer summen av neddiskontert nytte fra offentlige utgifter betinget på en budsjettligning. Felleskapet får skatteinntekter og finansinntekter fra finansformuen, og må fordele denne inntektsstrømmen over tid. For å fokusere utelukkende på handlingsregelen ligger andre valg en stat kan ta fast, eksempelvis skattesatser og porteføljens risikoeksponering. 

Det første resultatet er at hvis felleskapets diskonteringsrate er lik markedsrenten, og det ikke finnes andre midlertidige inntekter, skal realavkastningen på finansformuen brukes hvert år til å finansiere offentlig forbruk. Dette er dagens handlingsregel og følger av at felleskapet får mest nytte av formuen ved å fordele forbruket jevnt over tid. 

Gitt at modellen i sin enkleste form innebærer dagens handlingsregel er det nå verdt å utforske hvordan andre faktorer påvirker utformingen av handlingsregelen. Faktorene jeg legger til er andre midlertidige inntekter (petroleumsinntekter), befolkningsvekst, høyere fremtidige behov (aldring), produktivitetsvekst, konjunkturer og avkastningsrisiko. Høyere fremtidige behov er ment å fange opp endringer i for eksempel befolkningssammensetningen som påvirker marginalnytten av offentlige utgifter. Modellen er komplisert, og det er ikke mulig å utlede en eksplisitt løsning. I stedet løses modellen under en antakelse om tilnærmet linjæritet, noe som tillater at vi kan lære noe om hvordan hver faktor påvirker utformingen av handlingsregelen. 

Hovedresultatene kan oppsummeres som følger. To faktorer bidrar til at felleskapet bør øke fondsuttaket: Fremtidige petroleumsinntekter og produktivitetsvekst. Tre faktorer bidrar til at vi skal redusere fondsuttaket: Befolkningsvekst, fremtidige behov og konjunkturer. Avkastningsrisiko har to motstridende effekter og totaleffekten avhenger av fondets størrelse relativt til produksjon og preferanser. I hvert tilfelle utleder jeg en formel for hvor stor justeringen av uttaket skal være og hva denne justeringen avhenger av. Til slutt viser jeg at formlene er gode tilnærminger til de ikke-lineære løsningene fra numeriske simuleringer av modellen.

Modellen

Denne seksjonen presenterer modellen som brukes for å utlede optimale handlingsregler. Først diskuteres modellen i sin enkleste form der den nåværende handlingsregelen utledes. Deretter utvides modellen med flere faktorer som påvirker optimalt fondsuttak. 

En enkel modell for handlingsregelen

Den sosiale planleggerens (felleskapets) objektivfunksjon er den neddiskonterte nytten av bruk av offentlige utgifter  c

​ ${max}_{{\left\{c_t\right\}}_{t=0}^{\infty }}{\int }_0^{\infty }{e}^{–\rho t}u\left(c_t\right)dt$     (1)

som maksimeres betinget på budsjettligningen

​ ${db}_t= \left({rb}_t+ \tau y – c_t\right)dt.$     (2)

I ligningene er  b finansformuen,  y er produksjon,  τ er en skattesats,  r er realrenten og  ρer diskonteringsraten. Budsjettligningen fanger opp at inntektene  rb +τy som ikke brukes på offentlig utgifter  c vil spares i fondet  b. I tillegg antas det at løsningen må tilfredsstille en naturlig låneskranke.²

Nyttefunksjonen antas å tilfredsstille ​ u'(⋅) > 0​,  u»(⋅)<0​ og ​ u»'(⋅) > 0​. Løsningen på dette problemet er

$c = rb + \tau y + f\left(c\right)\left(\rho –r\right)$     (3)

der  f(c) > 0​ følger fra antakelsene om stigende og konkav nyttefunksjon.³

Offentlig forbruk er altså summen av finansinntekt og skatteinntekt hver periode, men i tillegg vil felleskapet bruke mer enn sine inntekter i dag hvis diskonteringsraten er høyere enn avkastningen på finansformuen. For å forenkle diskusjonen vil jeg i resten av artikkelen anta at  ρ = r, altså at felleskapets diskonteringsrate er lik markedsrenten.

Tilfelle 1. Den optimale handlingsregelen i sin enkleste form er

c = rb + τy.      (4 )

I den enkle modellen skal felleskapet bruke realavkastningen på fondet hver periode. Dette er dagens handlingsregel. Intuisjonen er at gitt en formue, ønsker vi å fordele bruken av formuen likt over tid. Dette gjøres ved at felleskapet kun bruker realavkastningen hver periode. 

En enkel utvidelse av modellen er at det finnes midlertidige inntekter ​ o_t​​ (petroleumsinntekter) som varer fra i dag til periode  T.

Tilfelle 2. Den optimale handlingsregelen med midlertidige inntekter ​ o_t​​ er

​ $c_t= r \left(\left(b_t+ {\int }_t^T{e}^{–rs}{o}_{s}ds\right)\right)+ \tau y.$     (5)

Nåverdien av midlertidige inntekter skal inkluderes som en del av finansformuen og felleskapets forbruk skal økes for å bruke realavkastningen også av denne formuen. Siden de fremtidige petroleumsinntektene fortsatt er relativt store taler dette for å øke fondsuttaket i dag. I praksis er derimot disse fremtidige inntektene usikre, noe som ikke er tatt hensyn til i ligning (5). Videre har det vært argumentert for at innfasingen av oljeinntektene bør skje gradvis.

Ligning (5) viser at begrepet formue egentlig inneholder dagens finansformue og nåverdien av fremtidige oljeinntekter. I diskusjonen av de utvidede modellene nedenfor kan man derfor tenke seg at finansformuen i det tilfelle representerer nettopp summen av fondet i dag og nåverdien av fremtidige petroleumsinntekter.

En utvidet modell for handlingsregelen

Modellen utvides nå for å ta hensyn til flere faktorer. Alle variablene i denne formuleringen er normalisert med befolkning og fremtidig behov. Den sosiale planleggerens objektivfunksjon er fortsatt den neddiskonterte nytten av bruk av offentlige utgifter c

​ ${max}_{{\left\{c_t\right\}}_{t=0}^{\infty }}{\int }_0^{\infty }{e}^{–(\rho –g_n–g_c)t}u\left(c_t\right)dt$     (6)

I ligning (6) er  ρ en diskonteringsfaktor, ​ g_n​​ er befolkningsvekst og ​ g_c​​ er vekst i fremtidig behov (aldring). Både befolkningsvekst og fremtidig behov antas å vokse eksponentielt med vekstrater ​ g_n og ​ g_c​​, der begge påvirker marginalnytten av konsum. Appendix A viser hvordan man kommer fram til ligning (6)-(9).

Felleskapet maksimerer nytten av offentlig forbruk under tre betingelser

​ ${db}_t= \left(\left(\left(r – g_n– g_c\right)b_t+ \tau y_t– c_t\right)\right)dt + {{\sigma }_r{b}_{t}dW}_t^b,$     (7)

​ ${dy}_t= \left(g_y\overline{y_t}– g_c{y}_t– \theta \left(y_t– \overline{y_t}\right)\right)dt + {{\sigma }_y\overline{y_t}dW}_t^y,$     (8)

$d\overline{y_t}=\left(g_y–g_c\right)\overline{y_t}dt.$     (9)

Den første betingelsen (7) er den offentlige budsjettligningen som sier at vekst i offentlig formue  b er summen av forventet avkastning ​​ (r- g_n – g_c)b ​ og skatteinntekter  τy minus forbruk  c. I tillegg finnes det avkastningsrisiko ​ σr​​ som innebærer at finansformue kan varierere uavhengig av uttak og innskudd. Avkastningsrisikoen er formulert som en geometrisk Brownsk bevegelse og innebærer at avkastningsrisikoen er symmetrisk rundt forventet avkastning.

Den andre betingelsen (7) beskriver utviklingen i produksjon $y$. For det første vokser inntekten med produktivitetsveksten ​ $g_y$, men faller relativt til det fremtidige behovet ​ $g_c$​​. Videre fanger (7) opp konjunktursyklusen ved at produksjon påvirkes av «sjokk» $d{W}_t^y$ til produksjonen, men konvergerer tilbake mot potensiell produksjon $\overline{y_t}$​​​. Ligning (9) beskriver hvordan produktivitetsvekst og vekst i det fremtidige behovet påvirker potensiell produksjon. Det antas hele veien at produktivitetsvekst er definert som vekst i produktivitet per person.

Problemet er satt opp for å kunne diskutere fem faktorer som påvirker offentlig forbruk: Befolkningsvekst $g_n$​​, endringer i fremtidig behov $g_c$​​, produktivitetsvekst $g_y$​​, konjunkturer ${\sigma }_y$​​ og avkastningsrisiko ${\sigma }_r$​​. Slik problemet er formulert kan det løses ved å sette opp den såkalte Hamilton-Jacobi-Bellman (HJB) ligningen

$\left(\rho –g_n–g_c\right)V\left(b,y,\right)$

$=\underset{c}{\max }u\left(c\right)+ V_b\left(b,y,\bar{y}\right)\left(\left(r–g_n – g_c\right)b + \tau y– c\right)$

$+ V_y\left(b,y,\bar{y}\right)\left(g_y\bar{y} – g_c y – \theta \left(y –\bar{y}\right)\right)$

$+ \frac{1}{2}{\sigma }_y^2{\bar{y}}^2 V_{yy}(b,y,\bar{y}) + \frac{1}{2}{\sigma }_r^2{b}^2{V}_{bb}(b,y,\bar{y}).$     (10)

Utledningen av HJB-ligningen for et tilsvarende problem er beskrevet for eksempel i Achdou mfl. (2022). Problemet har tre tilstandsvariabler: Formue, produksjon og potensiell produksjon, med tilhørende drift- og diffusjonstermer for formue og produksjon.

Problemet over kan løses for konsumligningen (løst under antakelsene $\rho =r$ og $y\approx \bar{y}$​) ved å derivere ligning (10) med hensyn på $b$ og bruke førsteordensebetingelsen ​ $u‘\left(c\right) = V_b(b,y,\bar{y})$ kombinert med omhyllingsteoremet

$c = \left(r–g_n –g_c + {\sigma }_r^2\right)b + \tau y + \left(g_y – g_c –\theta \tilde{y}\right)y\frac{V_{yb}}{V_{bb}}$

$+\frac{1}{2}{\sigma }_r^2{b}^2\frac{V_{bbb}}{V_{bb}}+\frac{1}{2}{\sigma }_y^2{y}^2\frac{V_{yyb}}{V_{bb}}.$     (11)

Her er ​  $\stackrel{}{y~}$​ definert som produksjonsgapet ​ ​ ​, altså prosentvist avvik av produksjon fra potensiell produksjon. Ligning (11) er fortsatt relativt komplisert. For å komme videre gjør jeg følgende tre antakelser. Først antar jeg at den optimale løsningen er omtrent lineær i formue og inntekt. Det vil si at jeg antar at løsningen har følgende form der $\stackrel{}{\mathrm{mpc}~}$​ er handlingsregelen⁴. Videre definere jeg ​ som andelen av offentlig forbruk som dekkes av uttak fra fondet fordi det viser seg at denne variabelen oppsummerer løsningen godt. Til slutt antar jeg at nyttefunksjonen er ​ ${\mathrm{u’}}^c$​ («CRRA»-nytte).⁵ Ligning (11) kan i så fall skrives som

$c\approx \left(\begin{array}{c}r–g_n–\frac{g_c}{\omega }+\left(g_y–\theta \tilde{y}\right)\frac{1–\omega }{\omega }+ {\sigma }_r^2\left(1–\frac{1}{2}\left(\gamma +1\right)\omega \right)\\ +\frac{1}{2}{\sigma }_y^2\frac{{\left(1–\omega \right)}^2}{\omega }\left(\gamma +1\right)\end{array}\right)b+\tau y.$(12)

Strengt tatt skal en handlingsregel som den over kun være en funksjon av tilstandsvariablene $b$, $y$ og ​ $\bar{y}$​. Ligning (12) er en funksjon av $\omega$, definert som ​ ​ $\frac{\widetilde{mpc}b}{c}$​, altså er den en implisitt funksjon av seg selv. Ligning (12) er derfor ikke egentlig en løsning på problemet, kun en tilnærming. Denne tilnærmingen viser seg derimot å være nyttig for å forstå hvordan hver av de fem faktorene (​ $g_n$​​, ​ $g_c$​​, ​ $g_y$, ​ ${\sigma }_y$, ​ ${\sigma }_r$) påvirker utformingen av den optimale handlingsregelen. I seksjon 4 viser jeg at den ikke bare er nyttig for å forstå intuisjonen, men også presis i mange tilfeller.

Optimale handlingsregler

I denne seksjonen diskuteres optimale handlingsregler under antakelsen om at kun den enkelte faktoren er inkludert for å kunne forklare intuisjonen bak hver faktors effekt på den optimale handlingsregelen. 

Tilfelle 3. Den optimale handlingsregelen med befolkningsvekst ​ g_n​​ er

​ $c =(r–g_n)b + \tau y.$     (13)

Når vi har befolkningsvekst må felleskapet ta hensyn til at størrelsen på befolkningen endrer seg. Siden felleskapet bryr seg om offentlig forbruk per innbygger betyr det at det finnes et større behov for finansformuen i fremtiden når befolkningen er større enn i dag. Denne oppdaterte handlingsregelen tar hensyn til dette ved å holde fondet konstant per innbygger ved å redusere fondsuttaket i dag.

Tilfelle 4. Den optimale handlingsregelen med fremtidig behov ​ g_c​​ er

$c =\left(r–\frac{g_c}{\omega }\right)b + \tau y.$     (14)

Økte fremtidige behov virker nesten tilsvarende som befolkningsvekst. Fremtidige behov er ment å fange opp at vi i fremtiden kan ha større behov for finansformuen, for eksempel fordi befolkningen aldres. Ved økt behov skal fondsuttaket reduseres fordi vi har større nytte av pengene i fremtiden enn i dag. Effekten avhenger av to størrelser: Hvor mye inndekningsbehovet vokser ​ g_c​​ og andelen av offentlige utgifter som i dag finansieres av finansformuen  ω. Intuitivt fanger dette opp at vi må ta mer hensyn til det fremtidige behovet hvis fondet er lite i dag fordi det innebærer at vi ikke bare må spare fordi vi har behov i fremtiden, men også fordi fondet må kompensere for at inntekten heller ikke følger veksten i det fremtidige behovet. Et konkret eksempel er en økning i antall pensjonister som innebærer at fondet ikke bare må dekke økte pensjonsforpliktelsene, men også at produksjonen, og dermed skatteinntektene, per innbygger faller når en mindre del av befolkningen jobber.⁶

Tilfelle 5. Den optimale handlingsregelen med produktivitetsvekst  g_y​​ er

​ $c =(r+g_y\frac{1–\omega }{\omega })b + \tau y.$​     (15)

Ved produktivitetsvekst ønsker vi å bruke mer av oljefondet i dag. Grunnen er at ved produktivitetsvekst så er vi rikere i fremtiden. Dermed er også skatteinntektene høyere i fremtiden, noe som innebærer at marginalnytten av fondsuttaket er lavere i fremtiden enn i dag, og det er bedre å bruke mer av fondet i dag. Effekten avhenger av to størrelser: Produktivitetsveksten $g_y$​​ og andelen av offentlige utgifter som finansieres av fondsuttak ​ $\frac{1–\omega }{\omega }$​. Intuisjonen er som følger: Planleggeren ønske å jevne ut det offentlige forbruket. Ved produktivitetsvekst vokser inntekten gradvis slik at planleggeren ønsker å bruke mer jo større fondet er relativt til offentlig forbruk, målt ved ​ $\frac{1–\omega }{\omega }$​.

Ligning (15) tar for seg en spesifikk form for produktivitetsvekst, at inntekten vokser eksogent mens nytten per krone av offentlig forbruk er konstant. Det er mulig å tenke seg tilfeller der det offentlig også blir mer effektivt, noe som innebærer at det fremtidige behovet samtidig faller. I så fall forsterkes effekten av produktivitetsvekst. I motsatt tilfelle er det også nærliggende å tenke seg at produktivitetsvekst i privat sektor vil drive opp lønningene i offentlig sektor uten at offentlig sektor blir tilsvarende produktiv slik at vi får mindre nytte per offentlig krone. I så fall vil produktivitetsvekst innebære en tilleggseffekt gjennom økning i behovet for offentlige utgifter i fremtiden og resultere i at løsningen er kombinasjon av ligningene (14) og (15).

I formuleringen av problemet antar jeg at produktivitetsveksten er eksogen og uavhengig av bruken av oljepenger. Det er mulig å tenke seg tilfeller der høyt offentlig forbruk påvirker produktivitetsveksten, for eksempel fordi arbeidsstyrken feilallokeres i større grad når det offentlige forbruket øker. Siden produktivitetsvekst alltid er ønskelig for den sosiale planleggeren vil en slik endogenisering av produktivitetsveksten føre til at fondsuttaket skal reduseres i dag. Men jeg har ikke analysert hvilke faktorer som eventuelt påvirker en slik justering.

Tilfelle 6. Den optimale handlingsregelen med inntektsrisiko ​ σ_y​​ er

$c =\left(r–\theta \tilde{y}\frac{1–\omega }{\omega }– \frac{1}{2}{\sigma }_y^2\frac{{\left(1–\omega \right)}^2}{\omega }\left(\gamma +1\right)\right)b + \tau y.$     (16)

Handlingsregelen med inntektsrisiko fanger opp to effekter. For det første, hvis inntektene er lave i dag (negativt produksjonsgap, ​  y~<0) skal vi bruke mer fra oljefondet i dag. Det motsatte gjelder hvis inntektene er høye. Fondsuttaket skal altså stabilisere offentlig forbruk over konjunktursyklusen. Denne effekten fanger ikke opp automatiske stabilisatorer eller Keynesiansk finanspolitikk der man gjerne øker forbruket i resesjoner, men kun at offentlig forbruk skal være stabilt over tid.⁷

Den andre effekten er at inntektsrisiko fører til at fondsuttaket skal være lavere enn det ellers ville vært. Denne effekten er større jo større inntektsrisikoen ​ ${\sigma }_y$​​ er og jo mer forsiktig felleskapet er. Forsiktighet eller forsiktighetssparingsmotivet fanges opp av parameteren $\gamma$ og styrer i hvor stor grad felleskapet ønsker å spare i dag fordi fremtiden er usikker. Betydningen av inntektskomponentene øker med hvor viktig skatteinntektene er for finansieringen av offentlig forbruk, som fanges opp av ​  $\frac{1–\omega }{\omega }$ ​.

Tilfelle 7. Den optimale handlingsregelen med avkastningsrisiko  σ_r er

$c =\left(r+ {\sigma }_y^2(1– \frac{1}{2}(\gamma +1\left)\omega \right)\right)b + \tau y.$     (17)

Ved avkastningsrisiko er det to motstridende effekter fordi avkastningsrisiko kan håndteres på to måter. Den første er å redusere størrelsen på finansformuen. En mindre formue innebærer at felleskapets inntekter er mindre utsatt for avkastningsrisiko. Den andre måten er å øke fondet fordi dette gir en større buffer mot avkastningsrisiko. Denne andre effekten avhenger av graden av forsiktighet i nyttefunksjonen, representert ved  γ.

Når formuen er liten (liten  ω) eller felleskapet er lite opptatt av forsiktighet (liten  ω) vil den første effekten dominere og det er ønskelig å ta ut mer fra fondet enn forventet avkastning for å redusere avkastningsrisikoen. Ved liten formue har vi relativt liten nytte av fondsuttak, men fondet bidrar til å øke risikoen til forbruket gjennom avkastningsrisikoen. Etter hvert som fondet vokser bidrar fondet i større grad til å forsikre oss mot avkastningsrisiko (og annen risiko) og det er ønskelig å ta ut mindre fra fondet for å sikre en større buffer mot avkastningsrisiko.

Mer uformelt kan man antyde at disse to effektene fanger opp to aspekter i debatten. På den ene siden kan man argumentere for at vi bør bruke pengene mens vi fortsatt har dem fordi vi kan miste dem i fremtiden. På den andre siden kan man argumentere at for å bevare fondet bør man bruke mindre i dag for å sikre at fondet ikke forsvinner. Ligning (17) veier disse hensynene opp mot hverandre.

Det er verdt å merke seg at avkastningsrisiko også kan håndteres ved å justere porteføljeandelene i fondet, som påvirker forventet realavkastning  r og risiko  σ_r​​. Det kan være ønskelig å bevege seg langs det man i finans kaller effektivitetsgrensen («efficiency frontier» på engelsk), altså at etter hvert som fondet vokser kan det være ønskelig å velge en annen kombinasjon av  r og ​ σ_r​​ ved å justere porteføljeandelene i fondet. I versjonen av modellen der man kun inkluderer avkastningsrisiko kan man regne ut optimal kombinasjon av  r og ​ σ_r​​ (blant kombinasjoner langs effektivitetsgrensen) betinget på fellesskapets preferanser.

Det kan være nyttig å påpeke at antakelsen om at avkastningen på fondet følger en geometrisk Brownsk bevegelse er en rimelig streng antakelse. Det innebærer at størrelsen på fondet følger (omtrent) en random walk, noe som betyr at et stort fall i verdien på fondet ikke forventes å reverseres. Historisk har store fall i finansmarkedene ofte reversert seg. En slik justering av prosessen for avkastning vil svekke forsiktighetsmotivet for sparing noe. 

En kontantstrømregel er en alternativ måte å håndtere avkastningsrisiko på, foreslått for eksempel av Holden (2022). En kontantstrømregel reduserer avkastningsrisikoen ved å ta ut den delen av variasjonen i priser som kommer fra endringer i diskonteringsraten. Gitt at det er mulig å operasjonalisere en kontantstrømregel vil en slik justering fungere omtrent som å redusere den relevante avkastningsrisiko i rammeverket i seksjon 2, men vil innebære at  r, forventet avkastning, varierer over tid.

Numeriske simuleringer av optimale handlingsregler

Handlingsreglene presentert over gjelder under antakelsen om at forbruksligningen er tilnærmet lineær. Det er velkjent at når problemet inkluderer risiko vil forbruksligningen være strengt konkav (Carroll og Kimball, 1996), dog nær lineær. I denne seksjonen simulerer jeg modellen numerisk for den optimale handlingsregelen der alle effekter og interaksjonseffekter inkluderes. 

I simuleringene bruker jeg en forenklet variant av modellen der befolkningsveksten, inndekningsbehovet og produktivitetsveksten ikke er med. Dette er gjort for å fokusere på hvorvidt ikke-lineæriteter, som utelukkende stammer fra inntekts- og avkastningsrisiko, er kvantitativt relevante for løsningen av handlingsregelen. 

En del parametere er like på tvers av simuleringene. Den forventede realavkastningen  rer satt til 3 prosent og tidsdiskonteringen  ρ er satt lik forventede realavkastningen. Videre settes inntektsprosessen slik at  σ_y er lik 0,01 og graden av gjennomsnittsreversjon i inntektsprosessen  θ til 0,50 for å fange en rimelig størrelse og lengde på konjunktursyklene. Skattesatsen  τ er satt til 0,40 fordi skatter og avgifter utgjør om lag 40 prosent av BNP Fastlands-Norge. Alle variabler er normalisert med produksjon.

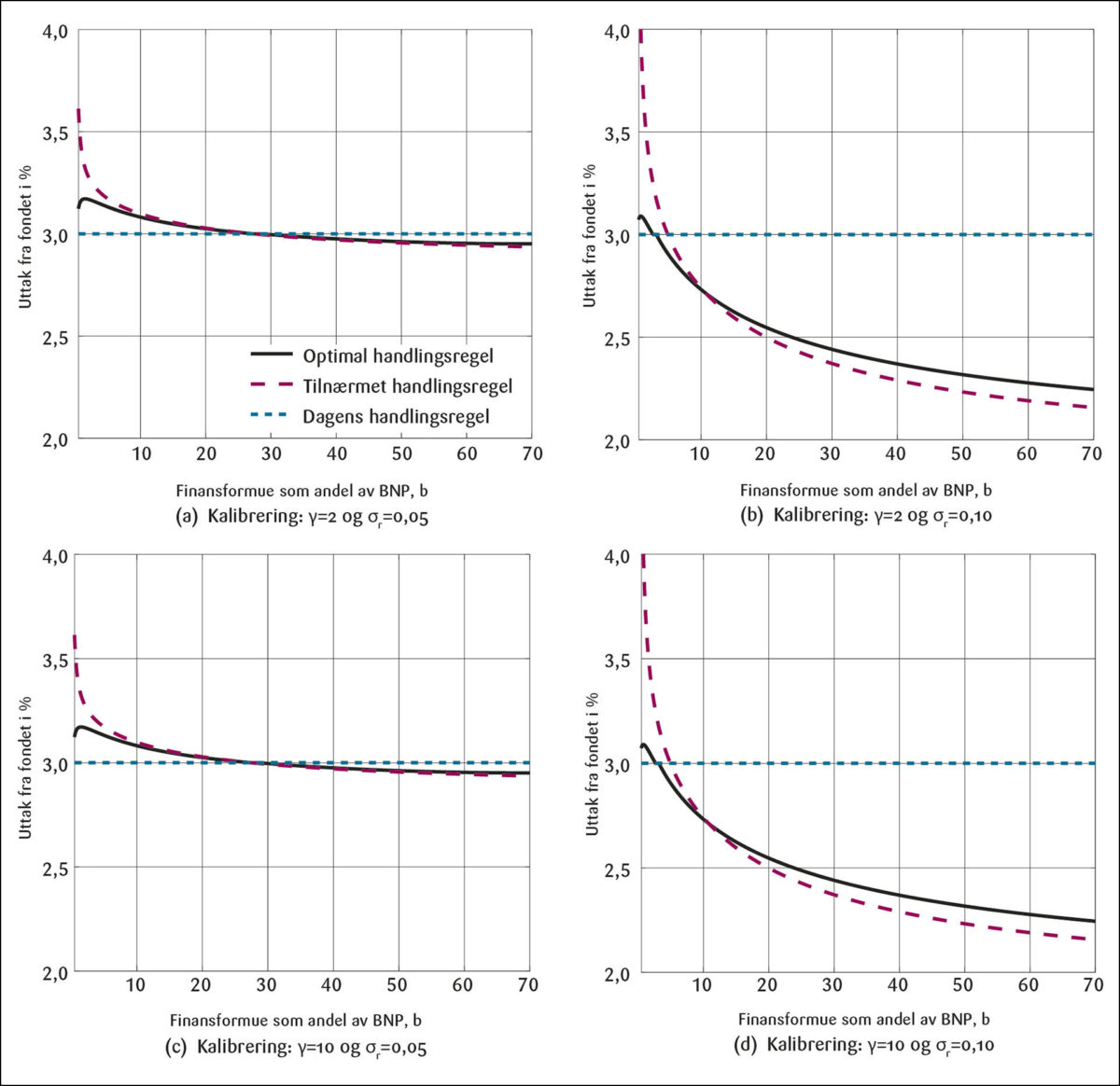
Figur 1 viser den optimale handlingsregelen sammen med tilnærmingen basert på ligning (12) og dagens handlingsregel (3 prosent). Simuleringene viser at den tilnærmede handlingsregelen er rimelig presis, særlig når finansformuen er stor. Videre illustrerer Figur 1 at verdien av  γ (som styrer forsiktighetsmotivet) har særlig stor innvirkning på den optimale handlingsreglen. Jeg bruker to verdier for  γ som tilsvarer vanlige kalibreringer i to litteraturer:  γ=2 (makro) og  γ=10 (finans). Mens handlingsregelen er nær 3 prosent uavhengig av formue og risiko når  γ=2, så synker den med størrelsen på finansformuen når  γ=10.⁸ I dagens situasjon, der oljefondet utgjør mellom 4 og 5 ganger fastlands-BNP, er den optimale handlingsregelen nær 3 prosent uavhengig av valget av preferanseparametere. 

Konklusjon

I denne artikkelen utledes et sett av optimale handlingsregler som tar hensyn til følgende faktorer: Fremtidige petroleumsinntekter, befolkningsvekst, fremtidige behov, produktivitetsvekst, konjunktursvingninger og avkastningsrisiko. Fremtidige inntekter og produktivitetsvekst bidrar til å øke fondsuttaket i dag. Befolkningsvekst, fremtidige behov og konjunktursvingninger bidrar til å redusere det optimale fondsuttaket. Effekten av avkastningsrisiko avhenger av fondets størrelse relativt til produksjon. En eventuell justering av handlingsregelen krever en større analyse der man mer presist kalibrerer de ulike faktorene og utleder robustheten rundt vurderingen. Samtidig bør det søkes å bevare den enkle utformingen av dagens handlingsregel i så stor grad som mulig.

A. Detaljer i problemformuleringen

Anta at felleskapets objektivfunksjon er

${\int }_0^{\infty }{e}^{–\rho t}{N}_t{D}_{t}u\left(c_t\right)dt$

der ​ $N_t$er størrelsen på befolkningen og ​ $D_t$​​ er en justering for fremtige behov (endring i marginalnytte over tid), mens ​ $c_t$​​ er konsum per person og behov $\left(\frac{C_t}{N_t{D}_t}\right)$​. Anta videre at ​ $N_t$ og ​ $D_t$​​ har følgende form

​ $N_t=e^{g_{n}t} \& D_t=e^{g_{c}t}$​

Det følger umiddelbart at objektivfunksjonen blir

${\int }_0^{\infty }{e}^{–\left(\rho –g_n–g_c\right)t}u\left(c_t\right)dt.$     (A.1 )

Videre utledes betingelsene i justert form. Definer ​ $b_t=\frac{B_t}{N_t{D}_t}$​​ ​, ​ $c_t=\frac{C_t}{N_t{D}_t}$​​ ​, ​ $y_t=\frac{Y_t}{N_t{D}_t}$​​ ​, og  ​​_ ${\bar{y}}_t=\frac{\overline{Y_t}}{N_t{D}_t}$​​ ​. Det følger fra Ito’s lemma

at⁹

​ ${db}_t= \left(\left(\left(r – g_n– g_c\right)b_t+ \tau y_t– c_t\right)\right)dt + {{\sigma }_r{b}_{t}dW}_t^r.$     (A.2)

Videre antar jeg at produktivitetsvekst ​ g_y og konjunktursyklene er definert for inntekt per person. I så fall får vi helt tilsvarende at

​ ${dy}_t= \left(g_y\overline{y_t}–g_c{y}_t – \theta \left(y_t– \overline{y_t}\right)\right)dt + {{\sigma }_y\overline{y_t}dW}_t^y,$     (A.3)

​ $d\overline{y_t}=(g_y–g_c)\overline{y_t}dt.$     (A.4)

Det justerte problemet er dermed å maksimere (A.1) under de tre betingelsene (A.2), (A.3) og (A.4), som beskrevet i teksten.

Fotnoter:

1. Takk til redaktør Rune Jansen Hagen, en anonym konsulent, Espen Henriksen, Steinar Holden, Knut Moum, Kjersti Næss Torstensen og Fredrik Wulfsberg for gode og konstruktive tilbakemeldinger. Email: m.b.holm@econ.uio.no. ↩︎
2. Her skal det være en formell i fotnoten ↩︎
3. Her skal det være formell i fotnoten ↩︎
4. Denne antakelsen holder ikke eksakt, men jeg viser senere at løsningen er presis i mange tilfeller. Løsningen vil være eksakt under såkalt «CARA» nytte, det vil si eksponentiell nytte. ↩︎
5. Antakelsen om nyttefunksjon kommer med noen kostnader. Det er for eksempel velkjent at en slik nytteformulering har problemer med å redegjøre for rimelige størrelser på både risikofri rente og forventede risikopremier. ↩︎
6. Dette økte fremtidige behovet er modellert noe enkelt i denne versjonen, der dette behovet er antatt å vokse eksponentielt. En mer naturlig justering kan være at behovet endrer seg over tid for eksempel fordi vi går igjennom demografiske sykler der andelen eldre er høyere i noen perioder enn i andre. I så fall er det relevante målet på om vi skal bruke mer i dag hvorvidt dette behovet i dag er høyere eller lavere enn gjennomsnittsbehovet i fremtiden. Er behovet i dag lavere enn gjennomsnittet vil det, som i ligning (14), være slik at vi ønsker å spare noe mer i dag. Det motsatte gjelder hvis behovet er høyere i dag enn gjennomsnittet. ↩︎
7. Keynesians politikk kan fanges opp, dog svært ad hoc, ved at også marginalnytten av offentlige utgifter øker i nedgangstider. ↩︎
8. Koder for å simulere modellen er tilgjengelig på forfatterens hjemmeside: https://www.martinbholm.com/. ↩︎
9. Her skal det være formell i fotnoten ↩︎